いつかは風を切って知る (境界層・層流・乱流・剥離)

さて、そもそも
層流翼とは何なのかを簡単におさらいしよう。

層流は
境界層(Boundary Layer)内の現象です。境界層というのは流体の持つ粘性により、(相対的に)静止した物体と速度を持つ流体との間に発生する層で、この層内では速度(圧力)が漸次的に変化しています。これを境界層内の
速度分布(Velocity Distribution)と呼びます。図では誇張していますが、実際の
境界層の厚さは数ミリ程度のものです。
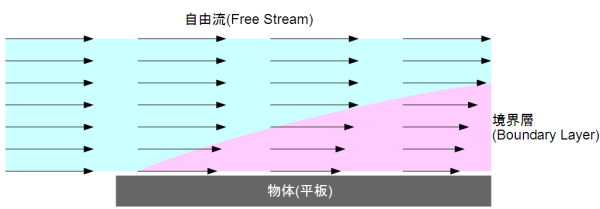 境界層
境界層
 層流(Laminar Flow)
層流(Laminar Flow)は境界層の状態を表す用語で、物体に沿って滑らかに流れている様子を示します。これに対し、 不規則な揺らぎを伴って流れている様子を
乱流(Turbulent Flow)と呼びます。境界層は物体に沿って流れるうち徐々に発達して乱流へと
遷移(Transition)します。また物体の形状などの条件によっては、流れは物体の表面を離れて
剥離(Separation)します。主翼面で起こる大規模な剥離現象は
失速(Stall)と呼ばれます。
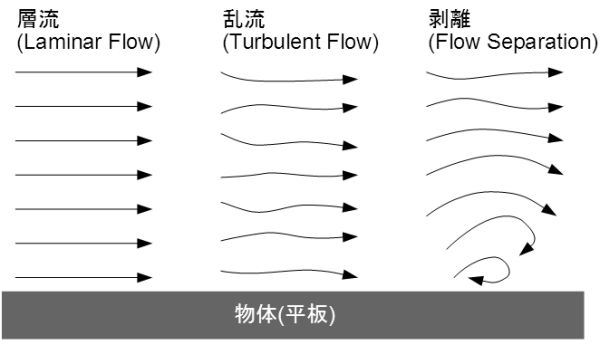 層流、乱流、剥離
層流、乱流、剥離

ここで
「遷移(乱流化)」と剥離(失速)」は違う現象であることに注意して欲しい。遷移が起きて乱流になっても境界層は維持されるし、逆に境界層が層流のまま剥離する場合もある。剥離はむしろ乱流のほうが起きにくい場合もある。現実の飛行機に見られるギザギザ板の
ボーテックス・ジェネレーターは意図的に乱流を発生させて剥離を防止する機構だし、ゴルフボールの表面に凹み(ディンプル)を付けてあるのも同じ理屈だ。
 ダグラス A-4 スカイホーク 主翼前縁と補助翼前のボーテックス・ジェネレーター
ダグラス A-4 スカイホーク 主翼前縁と補助翼前のボーテックス・ジェネレーター

境界層の発達に伴い、物体近傍の流速は段々遅くなって圧力が増大します。この様子を
圧力勾配(Pressure Gradient)と呼び、進むにつれて圧力が高くなる(正)ことを
「好ましくない圧力勾配(Adverse Pressure Gradient)」、逆に進むにつれて圧力が低くなる(負)ことを
「好ましい圧力勾配(Favorable Pressure Gradient)」と呼んだりもします。
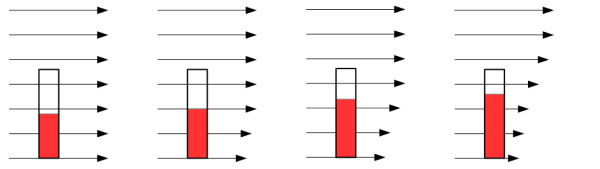 正の(好ましくない)圧力/速度勾配
正の(好ましくない)圧力/速度勾配
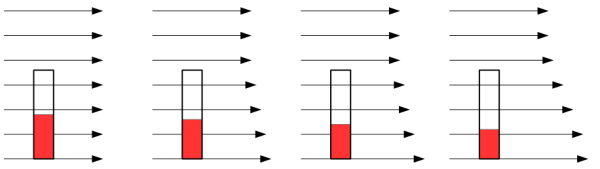 負の(好ましい)圧力/速度勾配
負の(好ましい)圧力/速度勾配

なんか、いきなり日本語と英語の対応が一杯出てきますね…。

Report 824 の原文を理解するには、流体力学の専門用語とそれが指すところの意味を把握していなければならないのだ。原文なんか読む気も無いよという人は関係ないと思うかもしれないが、もう少しだけ付き合って欲しい。

圧力勾配が正の場合、物体近傍の流速は段々減速してある点でゼロになり、そこから先では
逆流(Reverse Flow)します。逆流が発生するとそれは
渦(Vortex)になり、渦が発達するとやがて境界層は
剥離します。

逆流というのはつまり、空気を切り裂いて飛んでいる筈の翼面に空気が「貼り付いて」引っ張られて前に進む状態と考えても良い。しかし翼面から離れたところでは後ろ向きに流れているのだから、当然のように渦が発生するわけだ。
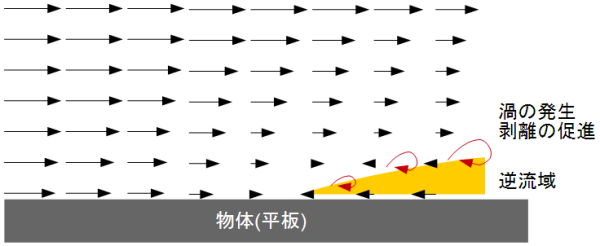 境界層の発達と逆流域・渦の発生
境界層の発達と逆流域・渦の発生

これに対し、乱流というのは境界層内で上下方向のエネルギー交換が起きている…いわば「さざ波」が発生している状態だ。物体近傍の流速は層流よりむしろ乱流のほうが高くなる。これに対し、剥離現象は物体近傍で著しい減速や逆流(渦)が起きている現象だ。繰り返すが、この二者を混同しないよう重ね重ね注意して欲しい。
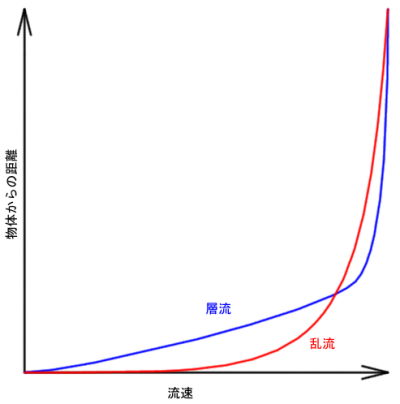 境界層内における層流と乱流の速度分布例
境界層内における層流と乱流の速度分布例

これ、実はマスターも勘違いしていたんですよね…(ぼそ)。

んー?!聞こえんなぁ?

・・・(^_^;)

さて、遷移(層流/乱流)と抵抗の関係は単純ではない。流れに置いた物体に発生する抵抗力は D=1/2ρv^2SCd で記されるが、抗力係数 Cd は定数ではなく流体の速度(厳密に言えばレイノルズ数)に応じて変化するのだ。しかもこの変化は必ずしも線形ではない。

円柱と平板のレイノルズ数と抗力係数の相関の一例を示します。レイノルズ数に対する抗力係数の変化を
スケール効果(Scale Effect of Drag Coefficient)と呼び、レイノルズ数増大に対して抗力係数が減少する現象を
「好ましいスケール効果(Favorable Scale Effect)」、増大する現象を
「好ましくないスケール効果(Unfavorable Scale Effect)」と呼びます。

平板ではレイノルズ数 10^5 を過ぎたあたりまで「好ましい」状態で、それを過ぎると「好ましくない」状態に逆転している。円柱では 10^4〜10^5 まではスケール効果がほとんど無く、そこを過ぎると一時的に「好ましい」状態が現われ、しかしすぐに「好ましくない」状態になっている。この非線形な挙動は境界層の遷移と剥離によるものだ。詳しい説明は省くが、「単純ではない」という事の意味を改めて思い出して欲しい。
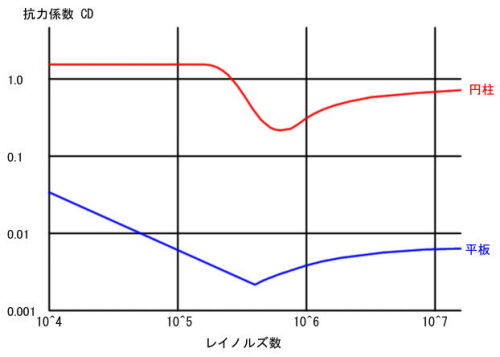 円柱と平板の抗力スケール効果例 (「10^X」は 10Xの代替表記)
円柱と平板の抗力スケール効果例 (「10^X」は 10Xの代替表記)

このスケール効果はあくまで
「抗力係数」に関するものであり、「抗力」でないことに充分注意してくれ。
抗力は流速の二乗に比例するので、流速が上がれば嫌でも大きくなる。しかしスケール効果が好ましい場合、速度に対する抗力の伸び率は二乗比例よりも下がり、好ましくない場合の伸び率は二乗比例よりも上がると理解してほしい。

開幕早々、難しい話がガンガン並んで頭が爆発しそうなんですけど…(涙)。

辛抱してくれ。世間一般的に抗力係数 Cd は定数として扱われることが多いのだが、これが関数であることを理解しておかないと層流翼の話はチンプンカンプンになってしまうのだ。

マスターも Report 824 読み始めの頃、その辺も理解してなくて、?(゜Д゜)?な状態になってましたよねー。

お前は何でそういつも一言多いかな…(怒)

ケンカはいいですから!
レイノルズ数について解説してくださいよ、どうして素直に「流速」って言わないんですか?!
 流体の挙動は速度だけではなく、大きさとも関係するから
流体の挙動は速度だけではなく、大きさとも関係するからだ。レイノルズ数というのは厳密には流体の慣性と粘性を示す無次元数なのだが、
航空工学では R=Vc/νで表される「翼弦レイノルズ数(Wing Raynolds Number)」を主用する。

V は流体速度(m/s)、c は翼弦長(m)、νは動粘性係数(m^2/s)。空気の動粘性係数は 1.5 x 10^-5 程度(湿度、気温、気圧によって変動)で、航空工学で扱うレイノルズ数の範囲は一般的に 10^6〜10^8 と言われています。

えーっと…二次大戦時の単発戦闘機クラスで翼弦長 1.8m と想定すると、R=10^6〜10^8 というのは V=8.3/ms〜830m/s(30〜3000Km/h)くらいの幅ということですか?後ろのほうは音速はるかに越えちゃってますが…。

c=1.8m に限定すればそうなるが、胴体全長にわたる挙動を扱うならもっと低い速度域でもレイノルズ数は大きくなるだろ?もっとも翼に関する議論では主に翼弦長を扱うので、R は 10^7 以下くらいまでしか扱わない。それは Report 824 のデータを見ていても判るはずだ。

ちなみに Report 824 では 6x10^6 や 20x10^6 など「10 の 6 乗」を基数に置いた表記になっていますが、これは 10 の 6 乗 = 百万 = 1000x1000 であり、英語では「ミリオン」科学表記では「メガ」として扱いやすい基数だからと思われます。

さて、流体力学における抵抗には
摩擦抵抗(Friction Drag、あるいは粘性抵抗 Viscous Drag)と
圧力抵抗(Pressure Drag)がある。剥離が起きないかぎり抵抗はすなわち摩擦抵抗だが、剥離が起きると物体後部に負圧が発生し、これに「引っ張られる」かたちで大きな圧力抵抗が発生する。

先に出てきたボーテックスジェネレータやゴルフボールのディンプルは、「剥離が起きるくらいなら乱流のほうがよっぽどマシ」「積極的に乱流を作ったほうが剥離が遅れて圧力抵抗が下がるので(゜∀゜)ウマー」という理屈ですね。

一方、
摩擦抗力係数は境界層の状態によって異なり、乱流よりも層流のほうが抗力係数が小さくなる。どのくらい小さくなるかはこれまたレイノルズ数によって異なるのだが、
飛行レイノルズ数域では概ね 1/4〜1/10 くらいだ。しかもその差はレイノルズ数の増大に応じて開く。つまり高速になるほど効果が大きくなる理屈になる。

やっと層流翼っぽい話になってきましたー(ほっ)。

境界層の遷移は物体の形状と関係する。流体が物体に当たる角度(迎角)や曲面が急だと遷移しやすく、極端な場合には剥離を引き起こす。
層流翼型は翼型前方の曲面を遷移を遅らせる形状に成型し、なるべく広い範囲(翼弦長)に沿って層流を維持することを狙った翼型だ。下に代表的な従来翼型(NACA 4 桁, 5 桁)と層流翼型を示す。出展は Report 824 の付録図(Supplemental Figures)からだ。
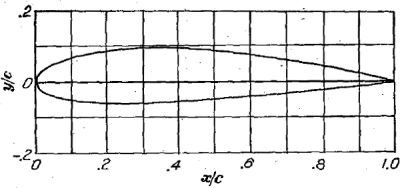 NACA 4 桁翼型 (2415)
NACA 4 桁翼型 (2415)
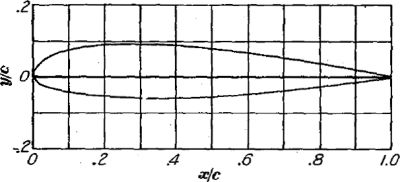 NACA 5 桁翼型 (23015)
NACA 5 桁翼型 (23015)
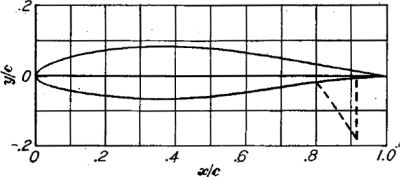 NACA 6- シリーズ層流翼型 (642-215)
NACA 6- シリーズ層流翼型 (642-215)

層流翼は
「主翼前縁の丸み半径が小さく、最大厚位置が後ろ寄り」という話はよく聞きますが、本当にその通りになってますねー。
 平板ならば圧力勾配は常に正(好ましくない)ですが、曲面では気流の加速が起きるため負の(好ましい)圧力勾配が発生します
平板ならば圧力勾配は常に正(好ましくない)ですが、曲面では気流の加速が起きるため負の(好ましい)圧力勾配が発生します。「最大厚位置が後ろ寄り」というのは負の圧力勾配をなるべく長い翼弦長に沿って維持させ、これによって境界層の発達と遷移を遅らせる意味があります。また「前縁の丸み半径が小さい」というのは気流が主翼に当たる迎角を下げる意味があると理解して良いでしょう。

層流翼型の形状理論は NACA Report 824 の前半に記されているので、興味がある人は自力で読解して頂きたい。今回はあくまで「P-51 層流翼伝説」を検証することを主眼に、層流翼型と従来翼型の性能とくに抗力係数の違いと、表面精度(平滑度)が及ぼす影響についての部分を読み取ってゆく。
I wish you (従来翼型との比較)

それにしても、膨大な情報量で何処から手を付けたらいいかわからないんですけど…(泣)。

まず
「従来翼型と層流翼型の性能比較」に注目してみよう。それに関するデータは p.17 の Figure.12(a)〜(e) に示されている。

これは…どう読むんでしょう?
 Figure.12 は各種翼型の、翼厚比変化に対する最小抵抗係数(minimum section drag coefficient)を記したもの
Figure.12 は各種翼型の、翼厚比変化に対する最小抵抗係数(minimum section drag coefficient)を記したものです。(a) が従来翼型、(b)〜(e) が 6- シリーズの層流翼型です。レイノルズ数は R=6x10^6。

NACA の翼型番号の意味について簡単にまとめると下の表のようになる。もっと詳しく知りたければこのへん
http://web.stanford.edu/~cantwell/AA200_Course_Material/The%20NACA%20airfoil%20series.pdf を参照してほしい。
NACA 4 桁型番
1桁目:キャンバーの曲率(%)
2桁目:最大曲率の翼弦位置(x10%)
3-4桁目:翼厚比(%)
例:NACA 2415 = キャンバー曲率 2%, 最大曲率翼弦 40%, 翼厚比 15%
NACA 5 桁型番
1桁目:最大揚抗比の揚力係数(x0.15)
2-3桁目:最大曲率の翼弦位置(x0.5%)
4-5桁目:翼厚比(%)
例:NACA 23015 = 最大揚抗比の揚力係数 2x0.15=0.3, 最大曲率翼弦 30x0.5=15%, 翼厚比 15%
NACA 6- シリーズ
1桁目:常に6
2桁目:最小圧力位置(最厚位置ではない)の翼弦位置(x10%)
括弧内の値:最大揚抗比を維持できる揚力係数の±範囲(x0.1)
3桁目:最大揚抗比の揚力係数(x0.1)
4-5桁目:翼厚比(%)
例:NACA 642-215 = 最小圧力翼弦 40%, 揚力係数範囲±0.2, 揚力係数 0.2, 翼厚比 15%

NACA 6- シリーズには「65,3-218」とか「65(318)-217」「65
3-218」「65
318-217」のような表記バリエーションがあります。- の後の数字は常に設計揚力係数と翼厚比。中の数字は1桁の場合は揚力係数範囲、3桁の場合は揚力係数範囲+変更部の翼厚比を示します。, や () や下付き文字は厚み分布のバリエーションで、詳しくは NACA Report 824 p.6 の記述を読んでください。
| 表記 | 最小圧力位置(翼弦 %) | 揚力係数範囲 | 変更部の翼厚比 | 設計揚力係数 | 翼厚比 |
|---|
| 65,3-218 |
50% |
±0.3 |
|
0.2 |
18% |
| 65(318)-217 |
50% |
±0.3 |
18% |
0.2 |
17% |
| 653-218 |
50% |
±0.3 |
|
0.2 |
18% |
| 65(318)-217 |
50% |
±0.3 |
18% |
0.2 |
17% |

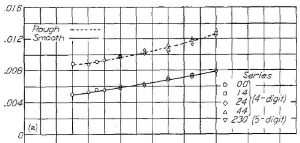
では Figure.12 に戻ってみよう。まず (a) は従来翼型のデータで、NACA 4 桁ナンバーが ○:00xx(対称翼), □:14xx, ◇:24xx, △:44xx の4種類、▽:5 桁翼型の 230xx について、6%〜24% の範囲で翼厚比(横軸)と最小抵抗係数(Cdmin)が比較されている。
|
(a) NACA 4 桁および 5 桁 |

|
(b) NACA 63- シリーズ |

|
(c) NACA 64- シリーズ |
|
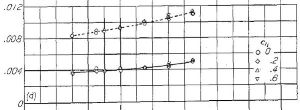
(d) NACA 65- シリーズ |
|
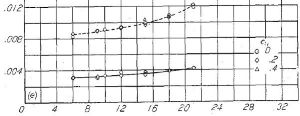
(e) NACA 66- シリーズ |
Figure.12 各種 NACA 翼型の、平滑と前縁荒面ありの場合の翼厚比と最小抗力係数の相関 R=6x10^6
(図をクリックすると別ウィンドウに拡大表示)

「Rough(点線の」と「Smooth(実線)」の2本が描いてありますが…。

「Smooth」は理想的平滑状態、「Rough」は翼弦 8% 位置に乱流源を置いたものだ。これについてはまた後で詳しく述べる。Figure.12(a) で注目すべきは、
従来翼型では翼厚比と抗力係数(CD)の相関はぼ同一線上にあるということだ。230xx が多少低い値を示してはいるが、例えば翼厚比 12% のとき「Smooth」で CD=0.006、「Rough」で0.095 付近にゴチャッと固まっているのがわかる。

NACA 4 桁でも 5 桁でも、
従来翼型の抗力特性は主に翼厚比で決定され、翼型による影響は殆ど無いんですね…。

従来翼型の Figure.12(a) に対し、Figure.12(b)〜(e)では NACA 63-, 64-, 65-, 66- シリーズの層流翼型について翼厚比 6〜21% までの抵抗値がプロットされています。丸や三角や四角のシンボルは翼型の最適揚力係数(CLi)で 0, 0.2, 0.4, 0.6 が示されていますが、概ね同じ範囲に収まっています。

ではそれぞれの「Smooth」について、6, 12, 20% の翼厚比から抵抗係数を拾ってみよう。数字の精度はコピーからの目読みだが、大筋はわかるはずだ。
従来翼型と層流翼型の抗力係数比較(前縁平滑)
| 翼厚比 | 6% | 12% | 20% |
|---|
| 従来翼型 | 0.005 | 0.006 | 0.007 |
|---|
| NACA63 | 0.004 (-20%) | 0.0045(-25%) | 0.0055(-21%) |
|---|
| NACA64 | 0.0035(-30%) | 0.0045(-25%) | 0.0055(-21%) |
|---|
| NACA65 | 0.0035(-30%) | 0.004 (-33%) | 0.005 (-29%) |
|---|
| NACA66 | 0.003 (-40%) | 0.0035(-42%) | 0.004 (-43%) |
|---|

えーっと…
最小圧力位置(最大厚)が後ろにある層流翼型のほうが抗力係数が小さく、最大で 43% に達する抵抗削減効果がある?

そういうことだ。これが「理想条件(風洞模型)における層流翼型の抵抗削減効果」になる。続いて「Rough」の方を拾ってみると下記のようになる。
従来翼型と層流翼型の抗力係数比較(前縁荒れ)
| 翼厚比 | 6% | 12% | 20% |
|---|
| 従来翼型 | 0.009 | 0.0095 | 0.0115
|
|---|
| NACA63 | 0.0085(-5.6%) | 0.009 (-5.3%) | 0.0105(-8.7%) |
|---|
| NACA64 | 0.0085(-5.6%) | 0.009 (-5.3%) | 0.0105(-8.7%) |
|---|
| NACA65 | 0.008 (-11.1%) | 0.0095(-0%) | 0.0110(-4.3%) |
|---|
| NACA66 | 0.0085(-5.6%) | 0.0095(-0%) | 0.0115(-0%) |
|---|

なんか気休めというか、ほとんど違いが無くなっちゃいましたー。

Smooth 条件では最小圧力位置を後ろに持って行ったほうが効果が大きかったのに、Rough 条件では翼弦 50% から後ろになると逆に効果が減っていますね。ただし
「悪くなっても従来翼型と同程度(1割程度は良い)」で、層流翼の抗力係数が乱流条件下で従来翼型より悪化するわけではない、という傾向も見えます。

これが「層流効果なんて風洞実験だけのもの、実機では良くて従来翼型と同程度」という話の出所なんでしょうか?でも、ここで言う「Rough」ってどの程度現実的なんでしょう…。

それについては後でじっくり解説する。うんざりするくらいにな。

あと「層流翼型は揚力係数が小さいから、抗力係数に大差が無いのであれば揚力係数の大きな従来翼型のほうが優れている」って話もありますよね?

それについては次の Figure.17 を参照してもらいたい。これは翼厚比 12% の従来翼型 NACA23012 に対し、64-, 65-, 66- の層流翼型の迎角−揚力係数変化(左側)と揚抗比変化(右側)をプロットしたものだ。
Figure.17 NACA 翼型数種の風洞空力特性比較
図をクリックすると別ウィンドウに拡大表示

○:NACA23012、□:64
2-415、△:65
2-415、▽:66(215)-416、◇:64
2-415(Standard roughness) です。

これも線が2本描いてあって、読み方がわからないですー。

グラフ左右とも水平に近い線はモーメント係数(Moment coefficient)で、とりあえずこれは置いておいてくれ。左側の斜め線が揚力係数/迎角比、右側のU字線が抗力係数/揚力係数比だ。

えーと、例えば迎角0度の揚力係数は、NACA23012 で約 0.12、6- シリーズの層流翼は上にゴチャッと固まっていて、おおむね 0.3〜0.35 くらい…あれ?
層流翼のほうが迎角に対する揚力係数が大きい?!

ただし Figure.17 では層流翼のほうが翼厚比が大きい(従来翼型の 12% に対し層流翼型は 15% および 16%)ので、
必ずしも翼型「だけ」の比較ではないことに注意してください。

注目すべきはむしろ、グラフの角度がほとんど平行だということだ。迎角に対する揚力の変化率、いわゆる揚力傾斜は従来翼型でも層流翼でもほとんど同じ。つまり
層流翼だからといって、離着陸時に従来翼型より何割も大きな迎角を取らなければならないということはない、と読むことができる。

もう一つは Figure.17 の左側で、グラフが右上で「垂れて」いる領域だ。これは大迎角での失速を意味している。NACA23012 は迎角 18 度、揚力係数 1.8 付近でストンと落ちているが、そこから先は 揚力係数 1.0 あたりで多少「踏みとどまって」いるのが読める。

層流翼は 64
2-415 rough(◇)が約 12 度で ヘタれ、他の層流翼型もおおむね 16 度付近でヘタれていますが、23012 ほど急激に落ちてはいないですねー。

グラフの右がカットされているので、失速後の特性についてはよくわからない。とりあえず
「層流翼は失速が急峻だ」とよく言われるが、Fiure.17(左) にはそれを検証するだけの情報は無いとだけ言っておこう。

次は右側の揚抗比を見てみよう。横軸が揚力係数・縦軸が抗力係数で、U字型のグラフ線は低いほど揚抗比に優れた翼型ということになる。

Figure.12(a) では従来翼型 230xx の翼厚比 12% のとき CD=0.006 でした。このグラフの○はCL=0.2〜0.6 の範囲で概ね CD=0.006 を示していますから、Figure.12 における従来翼の揚力係数も概ねこの範囲で、層流翼型の CL=0〜0.6 というデータと整合することがわかります。

・・・つまり?
 「層流翼型だから揚力係数が低い」とは一概には言えない
「層流翼型だから揚力係数が低い」とは一概には言えない、ということだよ。もっとも「層流翼型のメリットを活かそうとして設計揚力係数の低い翼型を採用した」例があったろうことは想像できるが。

つまり
層流翼にまつわる悪評の原因は、従来翼型 vs 層流翼型という話ではなく、単に揚力係数の低い翼型を使ったからではないか…ということですか?

少なくとも Report 824 を読む限り、6- シリーズ層流翼型の揚力係数が従来翼型に比べて著しく低いというデータは見当たらないのだ。揚力については後でもっと詳しく検証する。

では Figure.17(右)に戻ってみましょう。層流翼群はとりわけ揚力係数 0.2〜0.6 くらいの間で特に低い抵抗係数を出しており、最厚位置を後ろに置いた 66(215)-416(▽)が、翼厚比が一番厚い(16%)にも関わらず一番低い値を出しています。

でも、揚力係数 0.6 を超えると従来翼型(○)が緩やかに悪化してゆくのに対し、層流翼の揚抗比は急に悪化していますねー。
 層流翼には特に高い揚抗比を発揮する「スイートスポット(Low-drag range, 低抵抗域)」があるがその領域は狭く、そこより大きな揚力係数では従来翼より揚抗比が悪化する
層流翼には特に高い揚抗比を発揮する「スイートスポット(Low-drag range, 低抵抗域)」があるがその領域は狭く、そこより大きな揚力係数では従来翼より揚抗比が悪化するという傾向が読めるな。

本文では p.18 の右下に言及があります。要約すると「NACA 6- シリーズの層流翼型は高速飛行時の揚力係数域において NACA 23012 より大幅に低い抵抗を示しており、この優位はキャンバーの選択によって巡航速度域まで維持することができる。ただし大揚力係数域においては一般的に従来翼型のほうが 6- シリーズよりも抵抗係数が低い」となります。

ささきさんと大体同じこと言ってますねー。

当たり前だ!何ヶ月これと取っ組んできたと思ってるんだ。

ところで、◇のグラフは話にならないくらい悪い値ですが、これって…。

◇:64
2-415 Standrd roughness とは、前縁 8% 位置に乱流源を置いたものだ。

あー、さっき出てきた「Rough」の方の線ですか!64- シリーズの CLi=0.4 で翼厚比 15% だから、Figure.12(c) の横軸 15 と「Rough」のにおける△の交点というと…0.0095 くらい?

一方、Figure.17(右)で◇の線と横軸 CL=0.4 の交点は CD=0.0105 くらいです。10% くらい違いますね。

いや、ここは CL=0.4 との交点ではなく、グラフ最下点の値を拾うべきなのだ。Figure.12 の縦軸は縦軸は最小抗力係数 CDmin だから、その翼型の設計揚力係数における(CL=CLi)抗力係数ではなく、その翼型が示した最小の抗力係数を示していると解釈すべきだろう。

すると◇の最低点は CL=0.2 付近の 0.010 くらいですか?それでも Figure.12(c) とは完全には一致しませんが、5% くらいにまで近くはなりましたね。

これでピッタリ一致すれば「データのクロスチェックとはこう読むのだよ」とドヤ顔できたのだがな(苦笑)。理論値ではなく実験計測されたデータなので、5% くらいの誤差は含まれているのだろう。
風に負けないハート翼面のかたち (表面仕上げの影響)

さて、いよいよ p.22「Effect of surface irregularities on drag」に入ってゆくぞ。この少では以下の5項目にわたって実験と考察が行われている。
- 許容可能な表面の荒れ(Permissible roughness)
- 許容可能な表面の波打ち(Permissible waviness)
- 固定遷移における抵抗(Drag with fixed transition)
- 実機製法による抵抗(Drag with practical-construction methods)
- プロペラ後流と震動による影響(Effects of propeller slipstrim and airplane vibration)

あ…「実機製法による抵抗」って、ここに答えが書いてありそうな気が…。

慌てるなって。結論「だけ」を拾い読みするのは早合点と間違いのモトだぞ?。この章は「層流翼伝説」と「層流翼否定論」について重要な示唆を多く含んでいるので、じっくり解説してゆく。
許容可能な表面荒度(Permissive roughness)

この章の冒頭では「主翼表面の乱れは大きな抵抗源となることが知られている」「NACA 6- および 7- シリーズの層流翼では表面乱れに対する影響が更に大きくなる」と述べられている。続いて
大レイノルズ数域における表面状態を記述する正確な手法は確立されていないが、一般的な結論は得られている。
極論するならば、表面は鏡面のように磨き上げる必要はない。ラングレイの二次元低乱流風洞を用いた実験によれば、そのような研磨やワックス仕上げは、満足すべきサンドペーパー仕上げに対して向上を示さない。
ラングレイの二次元風洞における翼弦長 5〜8 フィートの大型翼型模型の場合、空力的に平滑な仕上げが必要な場合、表面を 320 番のサンドペーパーで翼弦方向に研磨した。

エリック・ブラウン氏の P-63 を用いた飛行実験の回想では「主翼前縁を 1/5000in 精度まで磨き込んだ」「地上では主翼前縁にカバーを被せ、離陸上昇後に投下した」「前縁に虫が付着したり給油ホースが当たっただけで抵抗係数は2倍にもなった」という記述がありますが、なんか雰囲気が違いますね…。
 「鏡面のように磨き上げる必要はない」
「鏡面のように磨き上げる必要はない」って書いてあるじゃないですか!やっぱり、実機でも層流翼って効果があったんじゃないですかー?!

だから焦るなってば。続きを行くぞ。
NACA 6- シリーズ翼型の風洞実験によれば、磨かれた表面上への突出物は、凹む場合よりも遷移源になる。例えば、粉塵は引っかき傷よりも(傷の縁部が突出しないかぎり)効率的に遷移を引き起こす。大レイノルズ数域においては、油に汚れた手で触った指紋跡に付着した粉塵でも遷移を引き起こすと考えられる。
乱流源による遷移は約 15 度の角度をもって下流に広がる。分散した突出物であっても、特にそれが主翼前縁に近ければ広範囲な乱流を引き起こす。これはすなわち、低抵抗が求められる場合、非常に慎重な平滑検査が必要であることを意味する。
実機サイズの翼型で遷移を引き起こすような突出物は手で触れて感じることができる。ラングレイの二次元低乱流圧力風洞では、翼型模型を素手で撫でて検査し、引っ掛かりを感じた場合は乾いた布で磨くという検査手順が取られた。

あぁ…これが
「指紋一つで特性パー」とか
「三角状に剥離する」の元ネタなんでしょうか。

ここで述べられているのは「油汚れへの粉塵付着」ですから、「層流効果なんて指紋一つで台無し」というのは大袈裟すぎますね。また「三角状に剥離」というのも、剥離と遷移を混同した記述です。15 度というのも微妙な角度で、例えば翼弦 1.8m で前縁に遷移源が付着した場合、翼弦 30% の下流では約 14cm 幅になります。

前縁の点状遷移源の分布がそれ以上の幅ならば、部分的にでも層流効果は得られる筈ですよね…虫一匹付いただけで主翼全面層流あぼーんとか、そんなの絶対おかしいですもんね!
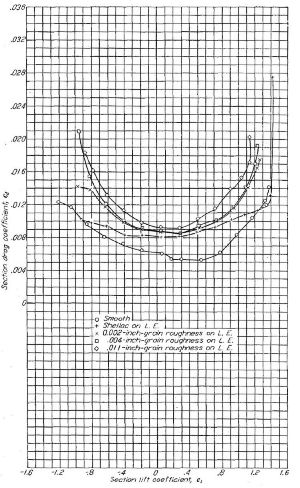
突出物による遷移の発生は外板波打ちとは異なり、突出点の直後から発生する。外板波打ちによる遷移はより下流で発生し、波打ちの大きさおよびレイノルズ数に応じて波打ち点に近づいてくる。Figure.19 は翼弦 5% に置いた円柱状の突出物が乱流遷移を引き起こす高さとレイノルズ数の相関である。このデータは比較的小さなレイノルズ数域で取得されているが、レイノルズ数の増大に伴って許容高さが急速に小さくなってゆく傾向を示している。このレイノルズ数との相関は Figure.20 において、迷彩ラッカー塗装仕上げがレイノルズ数 20x106 付近で抵抗急増しているデータとも符合する。
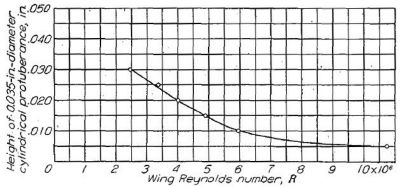 Figure.19 Figure.19 レイノルズ数と乱流遷移限界の円柱突起高さの相関
Figure.19 Figure.19 レイノルズ数と乱流遷移限界の円柱突起高さの相関
突起は 0.035 インチ直径で翼面に対し垂直に、翼弦長 90 インチ翼厚比 15% 最小圧力位置翼弦 70% の 6- シリーズ翼型模型の翼弦前縁 5% に置いた。
(図をクリックすると別ウィンドウに拡大表示)
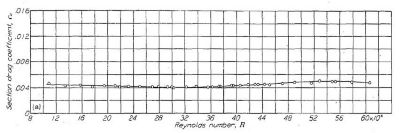 |
(a) 平滑表面 |
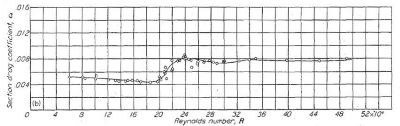 |
(b) ラッカー迷彩塗装の塗布後再仕上げなし |
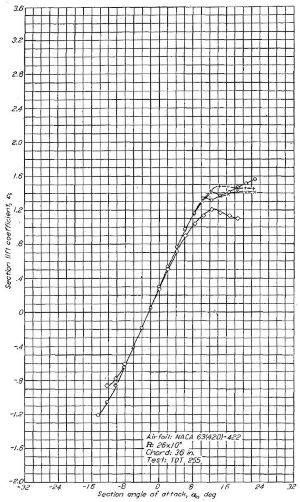
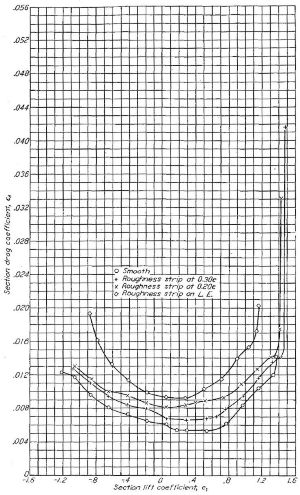
Figure.20 翼弦長 60 インチの NACA 65(421)-420 翼型模型におけるレイノルズ数と抗力係数の相関
(図をクリックすると別ウィンドウに拡大表示)

Figure.20 の迷彩塗料による抵抗増加が始まる R=20x10^6 に翼弦長 1.8m を適用すると 166m/s = 598Km/h、飽和域に入る R=24x10^6 だと 199m/s = 716Km/h となる。

うわぁ…レシプロ機の伸びしろが頭打ちになる速度域にがっつりですね。

大戦後期の P-51 が迷彩塗装を剥がして銀ピカになるわけです…。

迷彩塗装の影響については Figure.21 に追加のデータがある。ざっくり要約すると、層流翼型による低抵抗域は圧力勾配の変化(∝迎角)よりもレイノルズ数の増大によって狭まる影響が強く、その傾向は表面の荒度によって更に増大するとある。

・・・?!

速度が上がるほど・あるいは機体(∝翼弦長)が大きくなるほど、表面仕上げを平滑にしないと層流翼の「美味しいところ」は狭くなってしまう、という意味です。

つまり…
高速を狙って層流翼を採用しても、表面仕上げ精度が実現できなければ肝心の高速域に入る前に効果が無くなってしまい、しかも要求される精度は機体が大きくなるほど厳しくなると…。

そういうことだ。
許容可能な表面の波打ち(Permissive waviness)
 この項では冒頭「外板波打ちを平滑にするのは、表面仕上げを平滑にするより難しい」ことが述べられているが、「許容可能な波打ち具合」を定義することも難しいと述べられている。Figure.22 は測定された「波打ち具合」の影響の一例だ。
この項では冒頭「外板波打ちを平滑にするのは、表面仕上げを平滑にするより難しい」ことが述べられているが、「許容可能な波打ち具合」を定義することも難しいと述べられている。Figure.22 は測定された「波打ち具合」の影響の一例だ。
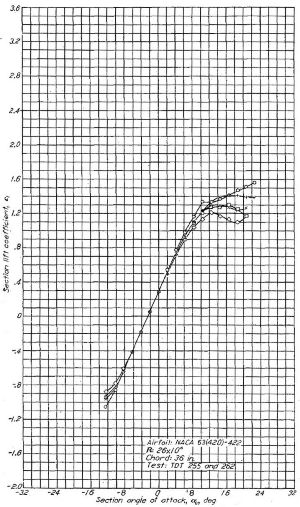
 Figure.22 は弦長 60in(1.54m)の翼型模型で、前縁約 30% を中心に全長 8in(20cm)にわたって深さ 0.05in(1.27mm) の凹みを設けた例です。「遷移点の前進と抵抗の増加はレイノルズ数 44x10^6 に至るまで顕著には現われない」、と書かれています。
Figure.22 は弦長 60in(1.54m)の翼型模型で、前縁約 30% を中心に全長 8in(20cm)にわたって深さ 0.05in(1.27mm) の凹みを設けた例です。「遷移点の前進と抵抗の増加はレイノルズ数 44x10^6 に至るまで顕著には現われない」、と書かれています。
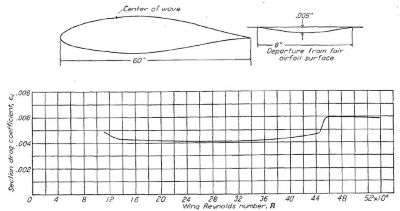 Figure.22 前縁に僅かな波打ちのある NACA 65(421)-420 横型における抗力係数変化の実験結果
Figure.22 前縁に僅かな波打ちのある NACA 65(421)-420 横型における抗力係数変化の実験結果
(図をクリックすると別ウィンドウに拡大表示)

R=44x10^6 だと c=1.8m のとき 365m/s=1314Km/h ですね。音速超えちゃってませんか?

うん、だから Figure.22 は「実用的に影響のない波打ちの例」なのだ。本文中には続けて「同じ弦長 60in の翼型模型において、長さ 2in 程度、高さ数千分の1in の複数の小さな波打ちによって、より低いレイノルズ数で遷移点の前進が発生する」と書かれている。不思議なことにこの「悪影響のある場合」のグラフは示されていない。

なんでそっちのグラフの方を出さなかったんでしょう…?

わからん。俺も翻訳しながら不思議に思った。

「For the types of wave usually encountered...」から後には
「実機製法による翼型の波打ちの検出には、直線定規(straightedge)を翼面に当て翼弦方向に回転させる評価法がある。定規が引っかかりなくスムーズに動くなら翼面状態は良好と考えられる。この手法では Figure.22 のような凹みは検出できないが、多くの実機製法翼型模型による実験の結果、直線定規による検査をパスした翼型は実用的に充分な仕上げ精度を持ち、飛行レイノルズ数域において低抵抗を示す」とあります。

なんか煮え切らない書き方ですねぇ。

その後は更に煮え切らないぞ。
「工作精度や翼型との一致精度を定量的に指定することは現実的ではない(it is not feasible)。表面仕上げに充分な注意が払われるならば、通常の工作精度指定(normal tolerance)において抵抗特性に大きな影響を与えない翼が実現できるであろう」。

何だか「結局よくわからないけど、きっと何とかなるよ!」と書いてあるようにも読めますねぇ…。

二次元翼型による風洞実験はかなり再現性が高いのだが、実機製法による三次元翼型は外乱要因が多くて相関性の実測が困難なのだろうな。それはこの Report 824 を通じて何度か言及されている。
固定遷移による抵抗(Drag with fixed transition)
 さて、こっちの項はもっとキッパリした書き方だぞ。そして、ここでは冒頭に出した Figure.12 について再言及されている。
さて、こっちの項はもっとキッパリした書き方だぞ。そして、ここでは冒頭に出した Figure.12 について再言及されている。
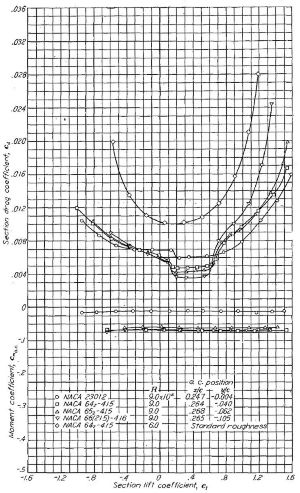
 Figure.23 は 63(420)-422 層流翼型において、前縁(Leading Edge, L.E) に様々な大きさの乱流源(grain)を付着させたもの。Figure.24 は翼弦 24in(61cm) の 63(420)-422 翼型に対し、幾つかの位置で標準乱流ストリップ(standard roughness strip)を付着させたものです。弦長 36in(91cm)、レイノルズ数 R=26x10^6。
Figure.23 は 63(420)-422 層流翼型において、前縁(Leading Edge, L.E) に様々な大きさの乱流源(grain)を付着させたもの。Figure.24 は翼弦 24in(61cm) の 63(420)-422 翼型に対し、幾つかの位置で標準乱流ストリップ(standard roughness strip)を付着させたものです。弦長 36in(91cm)、レイノルズ数 R=26x10^6。
 標準乱流ストリップとは 0.011in(0.27mm) 直径の粒を 5〜10% の密度で、翼弦比 0.08 の幅にわたって翼面上下に塗布したものと定義されている。これがどのくらい現実的なのかについては、「一般的な実機製法によって生じる工作荒れ、あるいは整備によって発生する荒れよりは大きく、しかし実戦機が前線で遭遇する氷や泥の付着、あるいは戦闘による破損よりは小さいと考えられる」とされている。
標準乱流ストリップとは 0.011in(0.27mm) 直径の粒を 5〜10% の密度で、翼弦比 0.08 の幅にわたって翼面上下に塗布したものと定義されている。これがどのくらい現実的なのかについては、「一般的な実機製法によって生じる工作荒れ、あるいは整備によって発生する荒れよりは大きく、しかし実戦機が前線で遭遇する氷や泥の付着、あるいは戦闘による破損よりは小さいと考えられる」とされている。
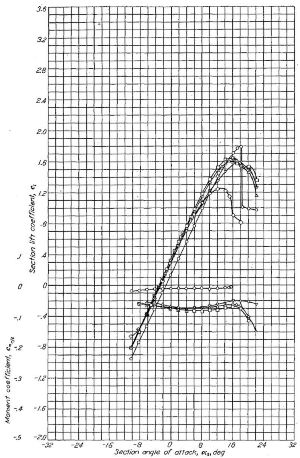
 Figure.23, 24 とも2枚1組のグラフとなっており、左側が迎角と揚力係数、右側が揚力係数と抵抗係数の関係を示しています。
Figure.23, 24 とも2枚1組のグラフとなっており、左側が迎角と揚力係数、右側が揚力係数と抵抗係数の関係を示しています。
Figure.23 NACA 63(420)-422 翼型における各種前縁状態の揚力抵抗特性
図をクリックすると別ウィンドウに拡大表示

Figure.23 では○:平滑、+:シェラック(ニス)塗布、×:0.002in(0.05mm)、□:0.004in(0.1mm)、◇:0.011in(0.27mm)の粒を前縁に貼っている。最小抵抗係数は○で 0.005、+で 0.008、◇では 0.009 付近まで増大している。

これがいわゆる
「層流効果なんてペンキ塗っただけであぼーん(死語)」という巷説の出所なんでしょうか。

注意しなければならないのは、
ここでの「ニスの塗布」は乱流源として前縁にスポットで塗られているもので、翼型全体に塗っているのではないことだ。塗装による影響の考察はすぐ後に出てくる。

本文中には「乱流遷移が前縁付近で発生する限り、乱流源の大小に関わらず大きな遷移が発生する。乱流源の大小による影響は揚力係数の増加に応じて拡大する」とあります。

なんか…+マークの右端ものすごく跳ね上がってるんですけど…。

これ失速の始まりじゃないかなぁ。左側のグラフだと+の揚力係数、迎角 15 度あたりからもう伸びてないだろ。

でも Figure.17 に比べると、いきなりガクンと落ちてはいませんね。Figure.17 が翼厚比 15-16% だったのに対し、Figure 23, 24 は 22% というかなりの厚翼だからでしょうか。

「層流翼の失速特性は急峻」という話はよく聞くのだけれど、Report 824 を読む限りそれを裏付けるデータは見当たらないんだよなぁ。さて、Figure.24 の方は乱流ストリップを○:なし、+:翼弦 30%、×:翼弦 20%、◇:前縁に貼り付けたものだ。
Figure.24 NACA 63(420)-422 翼型における 0.011 インチ粒の翼弦位置と揚力抵抗特性
図をクリックすると別ウィンドウに拡大表示

予想どおり、前縁に近いほど抵抗係数が増大していますね。

本文の方には「高揚力係数時における抗力係数は乱流源を前縁に置くと急増する」とある。Figure.24 の左図では◇は失速も早く起きているようだな。ここで Figure.12 への言及が登場するが、上で解説したことの繰り返しみたいなものだ。

要約すると「最小抗力係数の値は、4 桁および 5 桁型番の従来翼型より NACA 6- シリーズのほうが低い。翼厚増加に対する抵抗係数の増大は、「Smooth」より「Rough」のほうが大きくなる」となります。
 翼が厚いほど層流翼による恩恵が大きいのに、表面精度が悪いと「結局効果なし」になってしまう可能性もまた高い
翼が厚いほど層流翼による恩恵が大きいのに、表面精度が悪いと「結局効果なし」になってしまう可能性もまた高い…ということですか。

しかも翼弦が長いほど同じ対気速度でもレイノルズ数が大きくなるので、Figure.20 に示されたような表面荒度による抵抗急増の影響がより低い速度で発現してしまうことになる。

意外ですねー。常識的には、大型機になるほど表面仕上げの要求精度は下がりそうな気がするのですけど。
 「同じ形状でも、気流が外板に沿って通る距離が伸びるほど、境界層がよく発達して乱流になりやすい」
「同じ形状でも、気流が外板に沿って通る距離が伸びるほど、境界層がよく発達して乱流になりやすい」と考えれば良いんじゃないでしょうか。

えーっと…日本海軍機には翼型ばかりか胴体形状にも層流形状を取り入れた機体があって、特に試作に終わった偵察機 R2Y1 景雲なんか「それよりこの胴体を見てくれ、こいつをどう思う?」「すごく…層流翼です」なんですけど。

恵理子さん…そのネタって。
 空技廠 R2Y1 試製高速偵察機「景雲」
空技廠 R2Y1 試製高速偵察機「景雲」

主翼ですら層流が実現できずに四苦八苦しているのに、翼弦長が数倍に達する胴体でしかもプロペラ後流の真っ只中、まして前縁翼弦上に遷移どころか確実に剥離を引き起こす馬鹿でかい風防が突っ立っている有様では、層流もへったくれもないだろうな。

えーん(泣)。

雷電や強風の「延長軸を使ってカウリング前方をなだらかに絞った」紡錘形状胴体の効果がイマイチだったのも、この辺と関係ありそうな気がしますね。
実機製法に伴う抵抗(Drag with practical construction method)
 さて、いよいよ本丸だ。今までのデータの多くは二次元翼、つまり翼型の断面模型に対する風洞実験だったが、ここでは実機製法に基づく翼構造とその影響について考察されている。グラフも多いぞ。翻訳大変だ…orz
さて、いよいよ本丸だ。今までのデータの多くは二次元翼、つまり翼型の断面模型に対する風洞実験だったが、ここでは実機製法に基づく翼構造とその影響について考察されている。グラフも多いぞ。翻訳大変だ…orz
 ささきさんガンバ!リゲインあげますから、レッドブルも!
ささきさんガンバ!リゲインあげますから、レッドブルも!
 恵理子さん…ブラックだわ。
恵理子さん…ブラックだわ。
 まず Figure.26。これは「入念に作られた」翼型模型の実飛行および風洞テストで得られた揚抗比を示したものだ。上の線はレイノルズ数と揚力係数の相関を、下の線は揚力係数と抵抗係数の比つまり揚抗比を示している。
まず Figure.26。これは「入念に作られた」翼型模型の実飛行および風洞テストで得られた揚抗比を示したものだ。上の線はレイノルズ数と揚力係数の相関を、下の線は揚力係数と抵抗係数の比つまり揚抗比を示している。
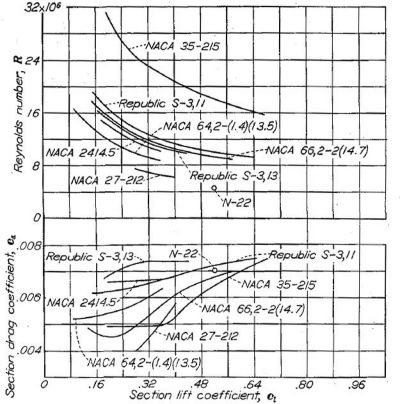 Figure.26 飛行実験によって得られた翼型の抗力係数比較。NACA 27-212 と 35-215 はグローブによる測定。
Figure.26 飛行実験によって得られた翼型の抗力係数比較。NACA 27-212 と 35-215 はグローブによる測定。
(図をクリックすると別ウィンドウに拡大表示)

揚力係数が小さくなるほどレイノルズ数(∝速度)が大きくなる?どういう意味ですか?!

(面積が同じであれば)発生する揚力が同じ、すなわち機体が水平飛行する前提で速度域を変えたものだと理解していいだろう。つまり揚力係数が大きい側では、機首を上げた大迎角の低速で飛んでいるということだ。

本文中では「これらの翼型は外板波打ちを最小にすべく入念な措置が取られた。ただし NACA2414.5, N-22, S-3,13, NACA27-212 についてはその限りではない」と記されています。

27-212 とか 35-215 とか、またわからない NACA の翼型番号が出てきました…。

これらは 6- シリーズとは異なる層流翼型らしいのだが、詳しいことは調べていない。35-215 と 27-212 のグラフは妙に他の翼型とかけ離れているのだが、注釈に「Test of NACA 27-212 and 35-215 sections made on gloves」とあり、測定条件が異なることが原因のようだ。

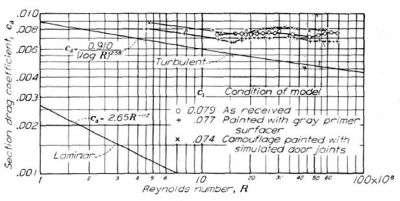
Figure.27 はより重要で、これはコンソリデーテッド・ヴァルティ(コンベア)社による 66(215)-1(14.5)実機製法翼型における、表面仕上げの各段階と揚抗比を示したものだ。
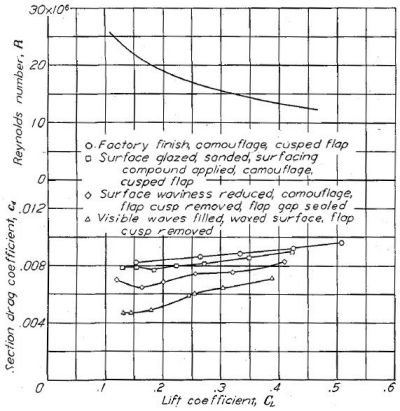 Figure.27 コンソリデーテッド・ヴァルティ社による NACA 66(215)-1(14.5)翼型に対する表面状態の影響測定。
Figure.27 コンソリデーテッド・ヴァルティ社による NACA 66(215)-1(14.5)翼型に対する表面状態の影響測定。
(図をクリックすると別ウィンドウに拡大表示)
|
○:工場仕上げ、迷彩塗装、フラップ突出あり
□:迷彩塗装、コンパウンド磨き仕上げ、フラップ突出あり
◇:迷彩塗装、外板波打ち低減、フラップ突出撤去+フラップ隙間埋め
△:外板波打ち平滑化(パテ埋め?)、フラップ突出撤去
|

隙間を埋めて磨いて…なんだか、エアレーサーの改造履歴を見るようですね。

でも、また翼型番号がよくわかりませーん(泣)。

最適揚力係数 0.1(±0.2)、翼厚比 14.5%(部分的に 15%) という意味だ。この辺の定義については p.6 を参照してくれ。

ともあれ、
工場仕上げ+迷彩塗装だと抵抗係数 0.008 以上、多少磨いた程度ではほとんど変わらず、パテ埋め磨き上げまでやってやっと 0.005、でも揚力係数が増加するとすぐに抵抗も増大する感じですね。

冒頭の Figure.12 と照らし合わせてみよう。Figure.12(e)では 66- シリーズの翼厚比 15% だと「Smooth」で 0.004 以下、「Rough」では 0.010 付近だから、
Figure.27 の実機製法模型は翼型模型の「Rough」より少し良いが理想状態からは全然遠い値で、パテ埋め磨き上げて揚力係数が低い時だけ「理想状態より少し悪い」程度に迫れる、ということになる。

エアレーサーの改造効果を実証するようなデータですね。しかし、こんな整備を戦場の実戦機に適用できるかは別の話ですが。

ま、また層流翼に不利なデータが…。

翼型模型では従来比 40% 以上の抗力低減効果が測定されているのに、測定条件を実機に近づけるほど「あれ?!」なデータが出てくる、というのが NACA Report 824 全体を通じての傾向だな。

p.27 の本文は「実機における層流翼の効果」についてかなり重要な示唆を含んでいるので、ほぼ全訳を示すぞ。
「航空機メーカーから納品された実機製法翼型は、採用した翼型に関わらず最小抵抗係数 0.0070〜0.0080 を示していた(Figure 28〜32)。現在の航空機製法において、これは良好な仕上げだと考えられる。翼面の平滑化は常に大幅な抵抗係数の減少を見せたが、ある程度の外板の波打ちは残った。試験に用いられた翼型模型のいずれも外板と前桁の結合部は平滑ではなかった。特別な措置が取られない限り、この波打ちは前桁部あるいはその直後から乱流遷移を発生させる。試験翼型のひとつ、Figure.10 の NACA 66(2x15)-116 はレイノルズ数 30x106 に至るまで良好な低抵抗特性を示した。この模型は翼弦 35% から先に桁を持たず、桁から前方には翼幅方向の強度材も持っていない。この構造によって非常に平滑な表面が実現でき、最新の高性能機にはこのような構造が採用されつつある。」
「実機製法模型において、翼型と抵抗係数の相関を正確に測定することは難しい。往々にして表面仕上げの差が翼型差以上の影響をもたらすからである。現実的なのは同一メーカーによって同時期に作られた別翼型模型を比較することであろう。Figure.30〜32 はそのようなペアの比較データである。これらのデータが示すのは、現在の航空機製法が取られる限り、軍用機が常用するレイノルズ数域において翼型の違いは比較的小さな効果しか示さないであろう、ということである。」

なんか…トドメ刺されちゃった感が。

p.22 では「鏡面のように磨き上げる必要はない」「320 番ペーパーの手磨きでも満足すべき結果が得られる」と書かれていましたが、実機と同じ骨格+外板のセミモノコック構造の場合、
「前桁から先の外板取り付け工法によって歪み(波打ち)が発生し、軍用機としては非実用的な処置(パテ埋め研磨)が取られないかぎり、層流翼型と従来翼型の間にはほとんど実用上の性能差は無い」と要約できますね。

手元にあった写真のなかで「古典的なセミ・モノコック主翼構造」がわかるのがこれだ。層流翼ではないがグラマン F7F タイガーキャット。主翼前縁付近に前桁があり、しかもそこで外板を継いでいる様子がよくわかる。主翼下面の反射からはリベットによる外板波打ちの様子が見て取れるだろう。
 グラマン F7F 戦闘機の主翼構造
グラマン F7F 戦闘機の主翼構造

うわぁ…層流効果あぼーん(死語)ですー。

一方、リノのハンガー前で分解されていた L-39 アルバトロスの主翼断面がこれだ。
 Aero L-39 ジェット練習機の主翼構造
Aero L-39 ジェット練習機の主翼構造

うわっ…板一枚の、しかも物凄い厚板構造!前縁内部にほとんど骨格がありません…。

遷音速に達する動圧に耐えるためもあるでしょうけど、板厚 1cm ちかくありますよね。こんな厚板の精密曲げ加工なんてどうやってるんでしょう。

これ以外にもチノの航空博物館で T-33 や L-29 デルフィンなど直線翼ジェット機の主翼前縁をしげしげと観察したが、確かに前縁近くを横切るリベットラインは無い。MiG-17 はエアショウ向けのピカピカ仕上げなので実戦機とはだいぶ違うだろうが、参考までに掲載した。
 ロッキード P-80
ロッキード P-80 |
 ノースアメリカン F-86
ノースアメリカン F-86 |
 Aero L-29 デルフィン
Aero L-29 デルフィン |
 PZL TS-11 イスクラ
PZL TS-11 イスクラ |
 MiG-17
MiG-17
|
 フォーランド・ナット
フォーランド・ナット |

「最新の高性能機にはこのような構造が採用されつつある」というのはそういう事なんですね。肝心の P-51 ムスタングはどうだったんでしょう…。

それについては後で考察することにしよう。さて p.28 に続く。
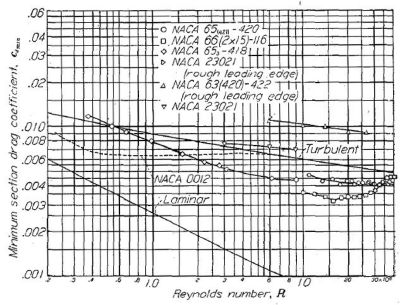
「大レイノルズ域においては、たとえ層流が実現できなくとも、表面の平滑化によって重要な抵抗の削減が得られる。乱流域においても表面荒度によって抗力が増大するとが知られている(資料 31)。表面荒度がもたらす抗力とレイノルズ数の相関を Figure.29 に示すが、ここでは通常大レイノルズ数域で期待できるスケール効果が現われていないことに注目されたい。このようなスケール効果は Figure.10 における、前縁部のみに乱流源を置いた 63(420)-422 と比較されるべきであろう。」
|
|
Figure.10 各種翼型におけるレイノルズ数と抗力係数の相関
平板における層流と乱流の摩擦抗力係数も共に示す。
|
Figure.29 NACA 23016 翼型の表面仕上げと抗力係数の相関
平板における層流と乱流の摩擦抗力係数も共に示す。
|
図をクリックすると別ウィンドウに拡大表示

どういう意味ですか?

改めて Figure.10 を見ると、層流翼でも従来翼でも、殆どの翼型は R=20x10^6 くらいまでは CD が右下がり、つまり「好ましいスケール効果」を示していますね。しかし Figure.29 を見ると、どの線も R=15x10^6 くらいまでは右下がりですが、あとはほぼ横這いです。

Figure.10 では前縁に乱流源を置いて「台無しにした」層流翼型でもレイノルズ数増大に対する抗力係数の減少…「好ましいスケール効果」が見られるのに、実機製法のまま磨きをかけていない Figure.29 ではそれが見られない…ということでしょうか。

そういうことだ。そしてすなわち「たとえ層流効果が得られなくとも、表面平滑度は抵抗係数に大きな影響を与える」という記述を裏付けるデータでもある。

Figure.34 は従来翼型と層流翼型における、防氷ブーツの装着による抵抗係数の増大を示している。理想状態では抵抗係数 0.004 vs 0.006 くらいだったのが、防氷ブーツの装着によって従来翼も層流翼も 0.007 くらいになっている。
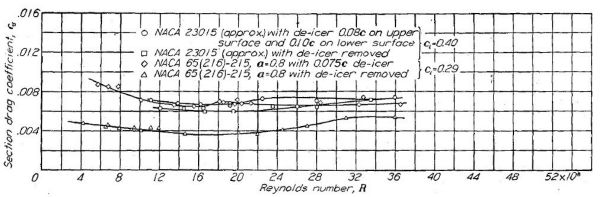 Figure.34 実機製法で製作された、比較的平滑な表面仕上げの翼型2種に対する防氷装置の影響
Figure.34 実機製法で製作された、比較的平滑な表面仕上げの翼型2種に対する防氷装置の影響
(図をクリックすると別ウィンドウに拡大表示)
 『層流翼の「スイートスポット(低抵抗域)」は前縁から翼弦 30% 程度までが平滑である場合にのみ発現し、それが乱れた場合には従来翼と同程度の特性になる』
『層流翼の「スイートスポット(低抵抗域)」は前縁から翼弦 30% 程度までが平滑である場合にのみ発現し、それが乱れた場合には従来翼と同程度の特性になる』という、今までの実験結果が再確認された格好ですね。
プロペラ後流と震動の影響(Effects of propeller slipstream and airplane vibration)
 この章ではあまり書くことはない。冒頭から「プロペラ後流と遷移の相関を示したデータは少なく、限られたデータも一定の傾向を示すとは限らない」と書かれ、震動については更に少ないと書かれているのだ。
この章ではあまり書くことはない。冒頭から「プロペラ後流と遷移の相関を示したデータは少なく、限られたデータも一定の傾向を示すとは限らない」と書かれ、震動については更に少ないと書かれているのだ。
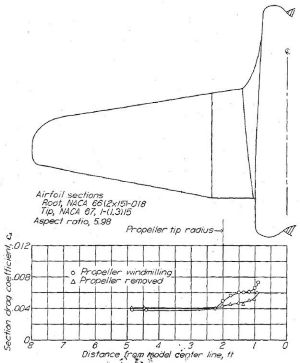
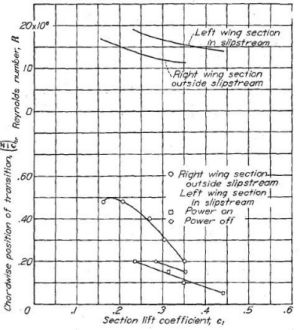
 プロペラについては Figure.35 に風洞実験(プロペラ空転)のデータが、Figure.36 に実飛行測定のデータが示されています。Figure.36 は右翼をプロペラ後流外、左翼をプロペラ後流内として遷移の発生位置が記されています。
プロペラについては Figure.35 に風洞実験(プロペラ空転)のデータが、Figure.36 に実飛行測定のデータが示されています。Figure.36 は右翼をプロペラ後流外、左翼をプロペラ後流内として遷移の発生位置が記されています。
|
|
Figure.35 航空機型模型のプロペラと翼型抗力係数の相関
CL=0.10; R=3.7x106.
図をクリックすると別ウィンドウに拡大表示 |
Figure.36 飛行状態における NACA 66- シリーズ翼の
プロペラ後流内と外での遷移の測定。
図をクリックすると別ウィンドウに拡大表示 |

これは…どう読むんでしょう?

プロペラ後流外の右翼:○では CL=0.17 のとき翼弦 50% で遷移が起こり、CL の増大(∝迎角の増加)に応じて遷移点が前進してゆく、すなわち層流効果が減少して抵抗が増える。後流内の左翼では□:パワー ON、◇:パワー OFF 時ともに遷移点は後流外よりも前進するが、それでも高速時には翼弦 20% まで遷移が起きていない、すなわち層流になっているという意味だ。

本文中では「Figure.35 は正確な測定ではないが、その結果は最前縁で遷移が起きて大抵抗が発生していることを否定するものであり、これは最近計測された Figure.36 の結果とも符合する」と書かれていますね。
 プロペラ後流内では層流効果は下がるけれども、完全に無くなってしまうわけではない
プロペラ後流内では層流効果は下がるけれども、完全に無くなってしまうわけではない…ということですね。

震動については「ラングレイの風洞実験では有意な影響が見られなかった」としながら、実機飛行試験では片発停止(フェザー)による震動で遷移点の後退が観測されたデータがある、としている。またエイムス研究所の実機大風洞では支柱の震動によって抵抗係数の逆スケール効果(Premature adverse scale effect)が観測されたとあるが…正直これもよくわからん。「遷移点の後退」は乱流遷移の遅れを意味する筈だが、Adverse scale effect というのは Favorable の逆、レイノルズ数増大に応じて抵抗係数が増大する相関を示し、それが Premature で起きたということは比較的低いレイノルズ数で遷移が起きたことを意味するのだから…。

…はい、リゲイン。

勘弁してください(泣)。

恵理子さん、いい加減にしないとマスター壊れちゃいますよ。まぁ、私はそれでも構わないんですけど。

お前らなぁ…!!
失速とか揚力係数とか最初に言い出したのは誰なのかしら?(揚力特性)

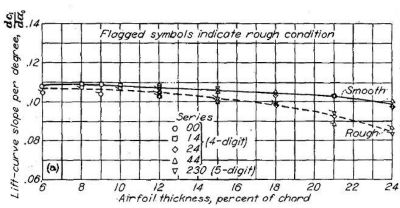
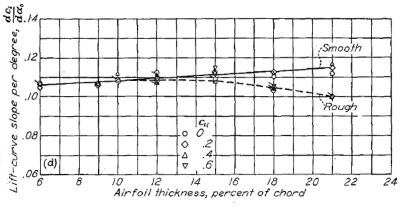
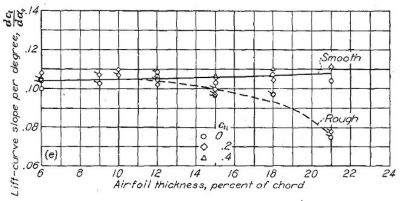
ここでは NACA 6- シリーズ層流翼型の揚力特性について、平滑な場合・前縁を荒らした場合・二次元翼(翼型模型)・三次元翼(飛行機模型および実機)についてかなり網羅的なデータが示されている。Figure.38 は迎角に対する揚力曲線傾斜(Lift-Cureve slope)の比較だ。
|
(a) NACA 4 桁および 5 桁 |
|
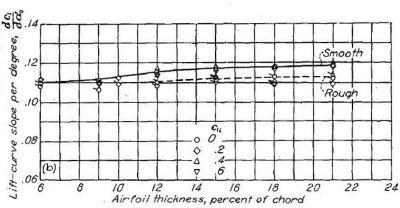
(b) NACA 63- シリーズ |
|
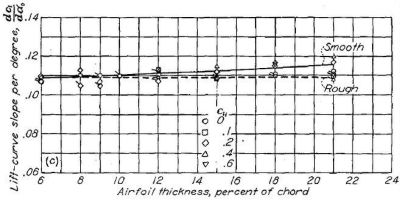
(c) NACA 64- シリーズ |
|
(d) NACA 65- シリーズ |
|
(e) NACA 66- シリーズ |
Figure.38 平滑状態と荒面状態における各種 NACA 翼型の翼厚・キャンバーと揚力曲線傾斜の相関。R=6x106.
(図をクリックすると別ウィンドウに拡大表示)

ここでも、6- シリーズ層流翼型の揚力特性が 4 桁・5 桁の従来翼型に劣るというデータは出ておらず、むしろ翼厚比の増大とともに優位になっています。ただし最小圧力位置(∝最大厚み位置)の後退に伴い、前縁が荒れた場合の揚力傾斜は悪くなりますが。

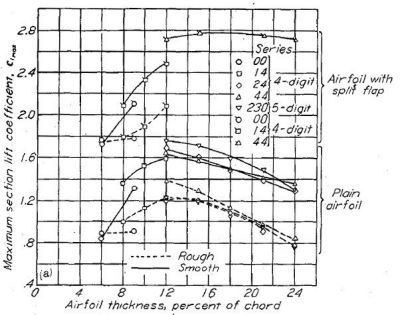
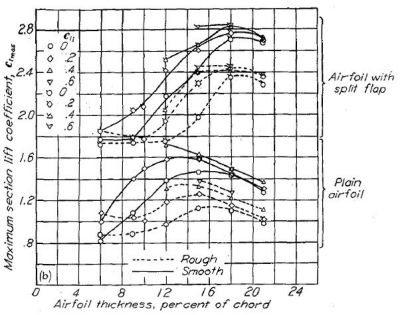
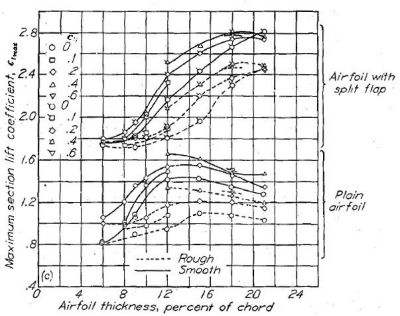
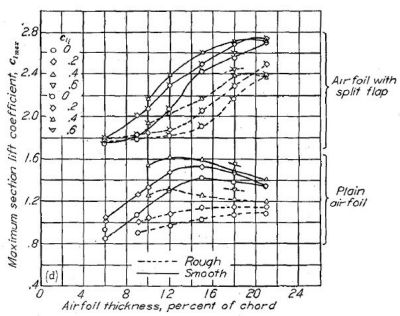
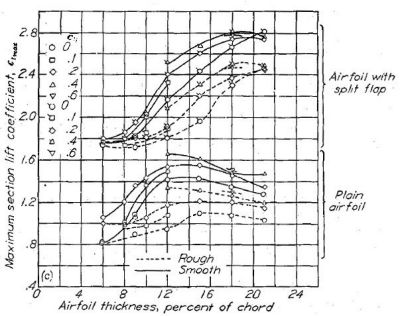
Figure.39 はフラップの有無を伴う、各種翼型の翼厚比(迎角ではなく)と最大揚力係数を示したものだが、従来翼(a)に対して 6- シリーズの層流翼(b〜e)の揚力係数が極端に低いという結果は出ていない。
|
(a) NACA 4 桁および 5 桁 |
|
(b) NACA 63- シリーズ |
|
(c) NACA 64- シリーズ |
|
(d) NACA 65- シリーズ |
|
(e) NACA 66- シリーズ |
Figure.39 平滑状態と荒面状態における、フラップ未使用・使用時の各種 NACA 翼型の翼厚・キャンバーと最大揚力係数の相関。R=6x106.
(図をクリックすると別ウィンドウに拡大表示)

ここでも「層流翼は揚力発生に不利」という通説とは異なる結果が示されていますね…。

この章の p.34 には失速特性に関する記述があるが、ここに層流翼の失速特性に関する重要な言及がある。
「NACA 230- シリーズのように最大キャンバーが前寄りの翼型は高い最大揚力係数を示していることを注記しておく。最大キャンバーが前寄りで翼厚比 6〜12% の翼型はふつう前縁から失速し、急激で大きな揚力損失をもたらす。より望ましい緩やかな失速は最大キャンバーを後ろにずらした通常キャンバーの NACA 24-, 44- および 6- シリーズのような翼型によって得られる。」

Figure.17 で NACA 23012 の揚力傾斜が失速後に急落していたのを裏付けるような記述ですね。

あっれーっ?!やっぱり
「層流翼は失速特性が急峻」って話と矛盾するじゃないですかー。

一般論として、翼型の前縁半径は大きいほど失速特性が緩やかに、小さくすると失速特性が急峻になると言われている。翼厚比やキャンバーが同程度であれば従来翼型より層流翼型のほうが幾分失速特性が悪いのかも知れないが、NACA Report 824 を読むかぎり、一概に「層流翼だから失速特性が悪い」とは言えないようなのだなぁ。ここでは 5 桁型番は悪く 4 桁型番は良好と記されているように、「従来翼型」とひと括りにもできない。

それじゃあ、スパイトフルで失速特性が悪化した原因は?!

正直わからん。エリック・ブラウン氏の回想によるとスパイトフルは失速時に横転する(Wing drop)悪癖があったとされており、単純な翼型の特性だけでなく、平面形状や捻り下げ、フィレットの処理やプロペラ後流などの複合要因ではないかと思われるのだが…「わからん」としか言えない。

ブラウン氏によればスパイトフルは主翼前縁半径を増大して失速特性を緩和したそうなので、NACA 6- シリーズよりも尖った翼型を採用していたのかも知れません。翼型は「スーパマリン 371」ということですが、詳しくはわかりませんね。

うーん…。ところで、Figure.45, 46, 47 には何処かで見たような飛行機の平面図が添付されていて、すごく気になるんですけど。

実はあんまり面白いものじゃない。Figure.45 は木型模型と実機の全機揚力傾斜比較、Figure.46 と Figure.47 は木型模型における前縁乱流源がもたらす全機揚力傾斜比較のデータだ。Figure.45 では実機で測定された揚力傾斜が木型模型より小さいことから隙間や歪みなど細部工作の重要性が説かれ、Figure.46, 47 では乱流源によって揚力傾斜が減少したこと、しかし最大揚力係数は Figure.47 ではかえって増加したことが言及されている。

なんで?何で乱流源を付けたら最大揚力係数が上がるんです?

それについては何の言及もない。ただ「一例では下がり、一例では下がった」と書かれているだけだ。だから「あんまり面白いものじゃない」って言ったろう。

ショボーン(´・ω・`)

それより気になるのは「保守的でない翼型(Unconservative Airfoils)」の記述だ。ここでは
「最近の流行として、特に長距離飛行を目的とする飛行機に高翼面荷重・高アスペクト比で翼根部の厚い翼型を採用するものが多いが、これは実戦状態で大きな抗力増大を招く危険がある」と警告している。

「高翼面荷重・高アスペクト比で翼根部の厚い長距離機」って…ボーイング B-29 ですか?

機種は明言されていない。ただ、Figure.12 が示すように風洞実験においては翼厚の厚い翼型でも抗力係数は大して増大しないが、表面が荒れると厚い翼の抗力係数は急増し、しかもその傾向は高揚力係数域において顕著になるため、過重運用や片発停止・戦闘損傷や着氷条件を考慮しなければならない飛行機では、むやみに厚い翼型を採用するのは緊急時の抵抗急増を招くとしている。

ボーイング B-29 の翼型はボーイング 117 型、翼厚比は翼根部 22%/翼端部 9% となっています。B-24 リベレイターが 22%/9.3% のデイビス翼型でほぼ同じ。従来翼型のボーイング B-17 が NACA 0018/0010、旅客機のダグラス DC-6 が NACA 23016/23012、ロッキード L-1049 が NACA 23018/4412 (いずれも末尾2桁が翼厚比)というのに比べると、B-24 や B-29 は翼根厚め・翼端薄めですね…。

それがここで述べられている「保守的でない」分類に含まれるのかはわからないが、こういった設計方針が 1940 年代の流行であったこと、この流行に対して 1945 年の Report 824 が警鐘を鳴らしていることには注目しておいて良いだろう。
あの空を回る風車の羽根たち (主翼設計への適用)

ここから後にはピッチングモーメント(揚力中心移動)、抗力中心移動、高揚力装置(フラップ)についての実験結果が書かれ、p.49 からは前縁吸気口や胴体との干渉についての考察と実験結果について記述されている。全部解説していたらそれこそキリがないし、いずれも「層流翼伝説」とは関係が薄いので割愛する。

興味のある人はぜひ原文を読んで、できれば翻訳をネットに上げてくださいね♪

ぶー。

p.51 からは主翼設計手法について言及されている。特に「翼型の選択について」は非常に示唆深い記述を含んでいるので、ここも全訳に近い形で解説しよう。
翼根部の選択について(SELECTION OF ROOT SECTION)
主翼の特性は翼根部に大きな影響を受ける。直線テーパー翼の場合は翼端に向かって翼型が変化してゆくが、主翼の大部分は翼根部の翼型に支配される。燃料や機材の格納、あるいは翼幅を確保するため、翼根部は可能な限り厚くすることが望まれることが多い。翼厚に対して抵抗係数は大きく変化しないこと、フラップによる大揚力が求められることから、翼根部の選択は最大揚抗比以外の特性で決定される。
高速機においては臨界マッハ数が最も深刻な制限になる。翼根部には胴体との干渉による流速増大が発生するため、想定される運用速度よりも大幅に臨界マッハ数の高い翼型の選択が望まれる。現在得られるデータは、臨界マッハ数と抵抗が急増するマッハ数の間にはわずかなマージンがあることを示す。航空機の速度がより高くなれば、薄翼化による抵抗急増を避けることは次第に困難になり、遂には不可能になる。

あ…これが名高い
「音の壁」ですね!
圧縮性の影響を考えない速度域の航空機においては、翼厚の限界は中〜高揚力時における、とりわけ表面が不平滑である場合の抵抗の増大によって制限される。翼型の選択は実機での表面状態が考慮されなければならない。軍用機においては特に泥や氷の付着や戦闘破損、多発機における片発飛行が考慮されなければならない。アスペクト比の増加を目的として翼根部を厚くする場合も、中〜高揚力時における現実的な表面処理状態における抵抗係数によって最適アスペクト比が定まり、それを超えて厚翼化しても性能はかえって低下する。

さっき出てきた「保守的でない翼型」の話ですね。

やっぱり「B-24 や B-29 って実は危ない設計」と言ってるような気がします…。
通常の航空機において翼根部はプロペラ後流の中にあって胴体とも干渉し、脚や兵装や整備パネルなども設けられる。そのため翼根部では層流効果を期待しがたい。このような条件が緩和されないかぎり、層流翼による抵抗削減は望めない。もし翼根部の厚みが大きい場合、大きな層流効果に期待しない 63- シリーズが優位を提供するであろう。

参考として XP-51 の翼型を示します。出典は NASA から公開されている Wartime Report Memorandum Report L6F12。翼型は 6- シリーズより前の層流翼型 NACA 45-100 とのことです。
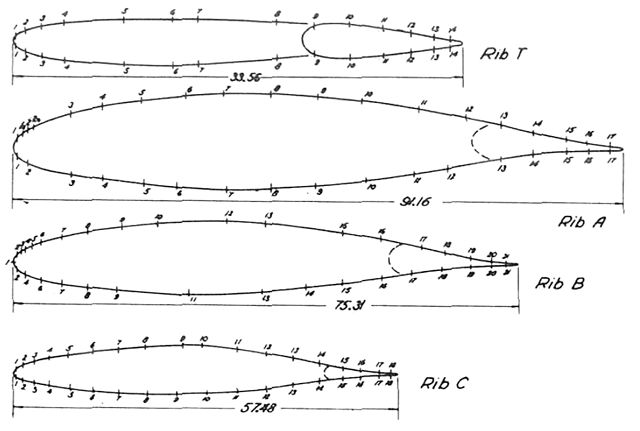 XP-51 翼型図。Rib.T は水平尾翼。Rib.A が翼根部, Rib.B は中間部, RIb.C が翼端部。
XP-51 翼型図。Rib.T は水平尾翼。Rib.A が翼根部, Rib.B は中間部, RIb.C が翼端部。

翼端部へ行くほど最厚位置が後退している…Report 824 の推薦通りですね!でも、XP-51 の設計って 1941 年じゃ?

Report 824 が書かれる 4 年前だが、その頃の NACA は既に、ここに書かれているような知見をある程度持っていたのだろうな。しかし同時に、この図面からは
小骨(Rib)が前縁にかなり集中している様子もわかる。これは上に述べられていたような鋲打ちによる外板波打ちを招くだろうな。

P-51 の主翼には平滑さを実現するため、鋲打ち後に切削研磨するリベットや平滑剤塗布を使用したといわれていますが、強度構造にまで遡った層流翼向きの設計にはなっていなかったようですね。
翼端部翼型の選択(SELECTION OF TIP SECTION)
良好な失速特性を実現するため、翼端部には大揚力係数と大きな迎角幅を持つ翼型が望まれる。失速特性も急峻でないことが望ましい。テーパー翼では翼端部のレイノルズ数が減少するため、大揚力係数の実現は翼根部よりも困難な場合が多い。このような場合、翼端部のキャンバー(曲率)を増加することが揚力係数増加に効果的である。多くの場合、キャンバーは高速時の抵抗特性や臨界速度の要求によって制限される。
翼端部のキャンバー選択は既存データから回答を得がたい困難を伴う。キャンバーによっては補助翼に大きな負荷が生じて横操縦性の困難と重量増大を招く。揚力中心を前進して補助翼の負担を減らすタイプのキャンバーは往々にして揚力係数を大して増大しない。NACA 230- シリーズのように最大キャンバーが前寄りの翼型では揚力係数も期待できるが、この場合は失速時に急激な揚力の減少が起き得る。エルロンによる主翼後縁キャンバーの変化に伴う主翼特性の影響は決して軽視してはならない。

学研の一式陸攻で片渕カントクが
「層流翼化には副次的に補助翼が軽くなる効果がある」と書いていましたが、この辺と関係あるんでしょうね。具体的にどうだ、というのはちょっとわかりませんが。
翼根部がじゅうぶん厚い場合、翼端部では翼厚比をある程度減らすことが望まれる。翼端部では胴体の干渉を受けないため、薄翼化することによって同じ臨界速度においてもより大きなキャンバーを与えることができる。薄翼化の限界は揚力係数によって制限されるであろう。
失速の抑制にはねじり下げ(Washout)も有効である。ねじり下げの限界は誘導抵抗によって制限されるが、1〜2 度の範囲ではその影響は小さい(資料 73)。ねじり下げはまた、高速飛行時に翼端部が低抵抗領域を逸脱してしまうことによっても制限される。翼型によっては、キャンバーを調整しなければねじり下げを与えることができない場合もある。
翼根部と翼端部で翼型を変えることは失速特性の改善と、翼端部で期待できる層流効果の活用に望ましい。例えば翼根部 NACA 230- +翼端部 NACA 44-、あるいは翼根部 NACA 63- + 翼端部 NACA 65- などが望ましいであろう。

…えっ。あれっ?!ちょっと待ってください、確か、日本海軍の空技廠は逆のことを推薦してませんでしたっけ?「厚みのある翼根部を層流翼化して、翼端部に向かうに従って通常翼型に近づけ翼端失速特性を改善する」という
半層流翼…D4Y 彗星や J2M 雷電が採用していましたが…。

Figure.12 を見ると「厚い部分を層流翼化する」というのは合理的に見えるのだが、翼根部は翼弦長が長いうえ実機では乱流源も多いので、肝心の層流効果による抵抗削減は期待しがたいだろうなぁ。先の「保守的でない翼型」で警告されているように、翼根部の翼型選定次第によっては逆効果にさえなるかも知れん。

うわぁ…(泣)

日本機の層流翼が効果を発揮していないように見えるのは、表面仕上げ精度だけでなく、この辺の知見にも差があったのかも知れませんね。

改めて XP-51 の翼型を見たら…空技廠式の半層流翼とは正反対ですね…。
翼型の選択やねじり下げの処理が適切でない限り、翼端部はいとも簡単に過大な負荷がかかって翼端失速を招く。この点において、過大なテーパー比や大きな後退角は望ましくない。この両者を組み合わせることは最悪であり、これによって引き起こされる翼端失速は横方向だけでなく縦方向の不安定性も招く。

大きなテーパー比と後退角といえばデルタ翼がありますが、デルタ翼は一般的に失速しにくい筈ですよねぇ…。

デルタ翼や LEX は前縁部からの翼端渦(wing tip vortex)が翼面上に流れることによる低圧で揚力を増加させ剥離を防止すると言われていますが、交叉流や渦を積極的に利用する空気力学の成立はもっと後のことだと思います。

1945 年ではさすがの NACA もデルタ翼や後退翼についての知見は不十分だったはずだ。ここで述べられているのはあくまで 45 年時点での結論であって、これに現代機を直接当て嵌めて考えるのは適切ではないだろうな。
Feeling Heart (結論)

さて、Report 824 もいよいよ結論だ。これも全訳を載せるぞ(しんど…)

ささきさんガンバ!(リゲインとレッドブルを渡しながら)
これまでのデータから、以下の結論が導き出せる。なお揚力、抗力、ピッチングモーメントなどの特性は 3〜9x106 のレイノルズ数域によって測定されている。
1. 翼面が平滑である限り、NACA 6- および 7- シリーズのような層流翼型は、高速飛行および巡航飛行での揚力係数域において、他の翼型より大幅な抗力の減少が実現できる。
2. 実機サイズの翼型模型を用いた場合、320 番のサンドペーパーで翼弦方向に研磨した程度の平滑度でも広範囲の層流を実現できる。また翼型の波打ちについては、前縁に直線定規を当てて滑らかに動く程度の仕上げ精度でも満足すべき結果が得られる。
3. 現在の航空機製造法に基づく中程度の翼厚比では、最小抵抗係数は 0.0080 程度が期待される。このような翼において、最小抵抗係数は翼型よりも表面仕上げ精度によって影響される。
4. 翼面の平滑化はたとえ広範囲の層流が実現できなくとも、大レイノルズ数域における抵抗削減に大きな効果がある。
5. 中程度のキャンバーを持つ NACA 6- シリーズの層流翼型の最大揚力係数は、NACA 24- および NACA 44- シリーズと大差ない。NACA 230- シリーズの揚力係数は 0.2 未満の翼厚比においてやや高い。
6. 中程度に厚い NACA 6- シリーズ層流翼のフラップによる最大揚力係数は NACA23012 と大差ないが、翼厚比が薄くなると大幅に低くなる。
7. NACA 6- シリーズの揚力曲線傾斜は NACA 24-, 44-, 230- シリーズよりやや高く、薄翼については理論値を上回る場合が多い。
8. 前縁部の表面乱れはフラップなし・60度下げいずれの場合も最大揚力係数の大幅な減少をもたらす。標準荒面帯による揚力係数の減少はフラップなし・60度下げの場合でほぼ同じである。
9. 前縁部の表面乱れは揚力傾斜の減少をもたらし、これは最小圧力位置を後ろに置いた翼型においてより顕著である。
10. 翼型特性を実機製法において期待される仕上げ条件で計測することは、実機の性能を予測する上で重要である。
11. 高速飛行および巡航飛行時の揚力係数域において、NACA 6- シリーズは従来翼型よりも臨界マッハ数が高く、臨界マッハ数域において充分な揚力係数を実現できる。
12. 中程度以上の揚力係数域においては、NACA 6- シリーズの臨界マッハ数は従来翼型に比べてそれほど高くない。しかし不十分なデータではあるが、臨界マッハ数域における NACA 6- シリーズの揚力係数は従来翼型に比べて満足できるものである。
13. NACA 6- シリーズ翼型は補助翼の装備について困難は認められない。
14. NACA 6- シリーズの干渉による境界層の剥離特性は、他の良好な翼型と同様である。剥離拡大を防ぐ最適なフィレット形状は場合によって異なるであろう。
15. NACA 6- シリーズには満足すべき前縁インテイクを設けることができるが、定番というべき手法は確立されておらず、実験に頼る必要がある。

…ふぅ。

お疲れ様でした。

おつかれさまでしたーっ!!
 みなさんごきげんよう。ウチュー人ささきである。
みなさんごきげんよう。ウチュー人ささきである。 アシスタントのメイド彩華です。
アシスタントのメイド彩華です。 突っ込みと合いの手の恵理子です。
突っ込みと合いの手の恵理子です。 …なんかノリが悪いな。
…なんかノリが悪いな。 仕方ないです。このコーナーの更新なんて何年ぶりでしたっけ?
仕方ないです。このコーナーの更新なんて何年ぶりでしたっけ? もう忘れちゃいました、あははーっ。
もう忘れちゃいました、あははーっ。 さて今回は、層流翼のお話である。「第二次大戦中の最優秀戦闘機」とも称えられる P-51 が層流翼を採用したことはよく知られており、その高性能は層流翼によって実現されたとも言われている。しかし…
さて今回は、層流翼のお話である。「第二次大戦中の最優秀戦闘機」とも称えられる P-51 が層流翼を採用したことはよく知られており、その高性能は層流翼によって実現されたとも言われている。しかし… しかし、「P-51 の高性能を層流翼に求めるのは間違いだ」という意見も根強いですね。
しかし、「P-51 の高性能を層流翼に求めるのは間違いだ」という意見も根強いですね。 うむ。例えば日本機ではほぼ同じエンジンを搭載した海軍の紫電改(層流翼型)と陸軍の四式戦闘機(従来翼型)に大した性能差は見られない。米軍では層流翼に換えた XP-47F が試作止まりだったり、英軍ではスピットファイヤを層流翼化したスパイトフル/シーファングが大した性能向上が無かった割に失速特性が酷いことになった、とも言われている。
うむ。例えば日本機ではほぼ同じエンジンを搭載した海軍の紫電改(層流翼型)と陸軍の四式戦闘機(従来翼型)に大した性能差は見られない。米軍では層流翼に換えた XP-47F が試作止まりだったり、英軍ではスピットファイヤを層流翼化したスパイトフル/シーファングが大した性能向上が無かった割に失速特性が酷いことになった、とも言われている。 なんか死屍累々ですー。
なんか死屍累々ですー。 層流翼否定派は「外板に付いた指紋程度の外乱で層流はいとも簡単に乱流に遷移してしまうので、層流翼は風洞模型だけの机上の理論倒れ。実用機では実現不可能」という意見を展開している。
層流翼否定派は「外板に付いた指紋程度の外乱で層流はいとも簡単に乱流に遷移してしまうので、層流翼は風洞模型だけの机上の理論倒れ。実用機では実現不可能」という意見を展開している。 その一方で、「翼全面で層流を維持するのは無理でも、部分的に層流が実現できれば数パーセントでも効果はあるはず」「層流翼が理論倒れならば、戦後の亜音速ジェット機に層流翼が採用されているのは何故か」という意見もありますね。
その一方で、「翼全面で層流を維持するのは無理でも、部分的に層流が実現できれば数パーセントでも効果はあるはず」「層流翼が理論倒れならば、戦後の亜音速ジェット機に層流翼が採用されているのは何故か」という意見もありますね。 両極端ですねー。
両極端ですねー。 実は、層流理論言い出しっぺの NACA が、1945 年 3 月 5 日付けでラングレイ記念航空力学研究所名義の詳細な報告書「NACA Report No.824 Summary of Airfoil Data」という報告書を提出している。今回のお題はこの Report 824 から、層流翼の理論と実態を定量的に読み取ってみようという趣旨だ。
実は、層流理論言い出しっぺの NACA が、1945 年 3 月 5 日付けでラングレイ記念航空力学研究所名義の詳細な報告書「NACA Report No.824 Summary of Airfoil Data」という報告書を提出している。今回のお題はこの Report 824 から、層流翼の理論と実態を定量的に読み取ってみようという趣旨だ。 Report 824 は複数のサイトから公開されています。グーグル検索で真っ先に挙げられるのは https://engineering.purdue.edu/~aerodyn/AAE514/Spring%202011/naca-report-824.pdf ですね。
Report 824 は複数のサイトから公開されています。グーグル検索で真っ先に挙げられるのは https://engineering.purdue.edu/~aerodyn/AAE514/Spring%202011/naca-report-824.pdf ですね。 だが、このコピーは2値スキャンで少々画質が悪い。もっと綺麗なコピーが NASA から公開されている。http://ntrs.nasa.gov/ から「NACA TR-824」すれば「Summary of Airfoil Data」として出て来るはずだ。同じ Test Report 824 なのにページ番号の振り方が全然違う。今回は NASA からダウンロードできる版をベースにするぞ。
だが、このコピーは2値スキャンで少々画質が悪い。もっと綺麗なコピーが NASA から公開されている。http://ntrs.nasa.gov/ から「NACA TR-824」すれば「Summary of Airfoil Data」として出て来るはずだ。同じ Test Report 824 なのにページ番号の振り方が全然違う。今回は NASA からダウンロードできる版をベースにするぞ。




 なんか、いきなり日本語と英語の対応が一杯出てきますね…。
なんか、いきなり日本語と英語の対応が一杯出てきますね…。


 お前は何でそういつも一言多いかな…(怒)
お前は何でそういつも一言多いかな…(怒) ケンカはいいですから!レイノルズ数について解説してくださいよ、どうして素直に「流速」って言わないんですか?!
ケンカはいいですから!レイノルズ数について解説してくださいよ、どうして素直に「流速」って言わないんですか?!












 さて、いよいよ本丸だ。今までのデータの多くは二次元翼、つまり翼型の断面模型に対する風洞実験だったが、ここでは実機製法に基づく翼構造とその影響について考察されている。グラフも多いぞ。翻訳大変だ…orz
さて、いよいよ本丸だ。今までのデータの多くは二次元翼、つまり翼型の断面模型に対する風洞実験だったが、ここでは実機製法に基づく翼構造とその影響について考察されている。グラフも多いぞ。翻訳大変だ…orz

 隙間を埋めて磨いて…なんだか、エアレーサーの改造履歴を見るようですね。
隙間を埋めて磨いて…なんだか、エアレーサーの改造履歴を見るようですね。
























