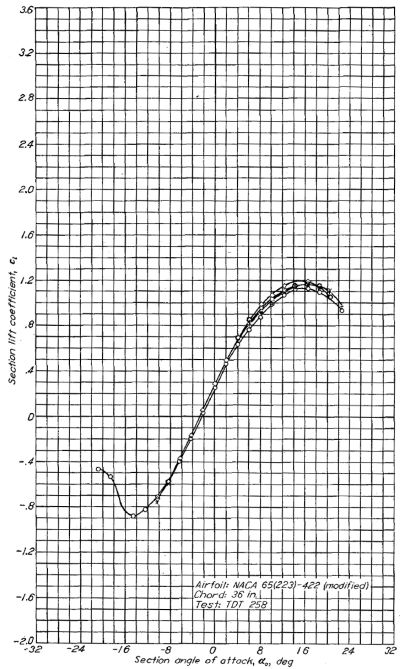
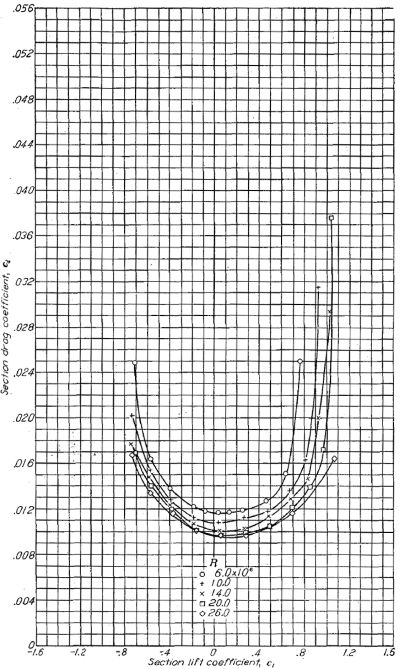
はじめに
本ドキュメントは
NASA のドキュメント・アーカイブ・サイト から公開されている NACA Report 824 "SUMMARY OF AIRFOIL DATA" の一部(層流翼の抗力と揚力に関する記述および結論)を「ささき」が個人的に翻訳し、「Vought Ishibashi」氏の運営する WEB サイト
「Warbirds」の場をお借りして公開しているものです。NASA は原則として公開ドキュメントに著作権を主張していません。本ドキュメントについても翻訳者「ささき」は著作権を主張しないのと同時に責任も持ちませんので、ご自由にお使いください。
NATIONAL ADVISORY COMMITEE FOR AERONAUTICS
REPORT No.824 SUMMARY OF AIRFOIL DATA
By IRA H.ABBOTT, ALBERT E. von DOENHOFF and LOUIS S. STIVERS, Jr.
Langley Memorial Aeronautical Laboratory Langley Field, Va.
総括(SUMMARY)
近年測定された飛行実験および風洞測定の翼型特性は可能な限り関係づけて収録した。飛行実験は主に後流観測法による抵抗の測定である。翼型特性の多くはラングレイの二次元低乱流圧力風洞で測定された。NACA 6- シリーズ翼型の応用に必要となる詳細なデータは、NACA 00-, 14-, 24-, 44- および 230- シリーズの測定結果とともに付録図(Supplementary Figures)に示されている。NACA 6- および 7- シリーズの翼厚形状を算出する数式は、それに関連する圧力分布式と共に示される。NACA 4 桁, 5 桁, 6- および 7- シリーズの圧力分布を迅速に推算する数式とデータが示される。
本報告には翼型の揚力・抵抗・ピッチングモーメント・臨界速度の特性解析が、表面状態との関連と共に含まれている。横方向の操縦機構(エルロン・スポイラー)、前縁吸気口、干渉に関する問題について軽く言及されている。これらのデータは表面仕上げの状態が翼型と少なくとも同程度には揚力と抗力の特性に影響を与えることを示しており、翼型選定や主翼特性推算において考慮されるべきことを示している。NACA 6- シリーズのような大規模な層流発生を可能とする翼型は、表面仕上げが充分に平滑である場合にのみ、高速飛行時および巡航飛行時に高い揚抗比を発揮し得る。NACA 6- シリーズは臨界速度特性も好ましく、高揚力装置や横操縦機構の取り付けに関わる問題も出ていない。
はじめに(INTRODUCTION)
これまでに、非常に多くの翼型に関するデータがラングレイの二次元低乱流圧力風洞によって測定されてきた。データは他の風洞や飛行実験からも、また高揚力装置の有無・表面仕上げの不均一・干渉の影響も含めたデータも採取されている。翼型がエルロンに使用された場合の特性データもある。これらの多くは公表されているが、それが分散していたことと個々の実験目的が異なっていたために、それらの相関を解析するまでには至っていなかった。本報告書の目的はこれらのデータを可能な限り総括し関連づけ相関を見出すことにある。
本報告には NACA 翼型に関する最新の空力特性が示される。NACA 翼型の歴史的経緯についても僅かに触れている。翼型の圧力分布を迅速に推算する手法について、古い NACA 4 桁, 5 桁翼型と 6- シリーズ翼型の新しいデータが含まれる。NACA 6- および 7- シリーズの翼厚形状を算出する数式は、それに関連する圧力分布式と共に示される。翼型の応用設計に必要な詳細なデータは巻末に付録図と共に示される。本報告には翼型の揚力・抵抗・ピッチングモーメント・臨界速度の特性解析が、表面状態との関連と共に含まれている。高揚力装置については現在わかっているデータが示される。横方向の操縦機構、前縁吸気口、干渉に関する問題については、応用設計に伴う空力的問題とともに軽く言及されている。
図番つきの図は本文中から参照される様々なデータを示す。付録図と表は番号が振られていないが、巻末に翼型番号と頭文字で整理されている。
I - 基本厚み形状
II - 基準線データ
III - 翼型の縦座標
IV - 予測される臨界マッハ数
V - 各種翼型の空力特性
これらの付録図と表は翼型の基本データを提供する。
表記について(SYMBOLS)
(省略)
歴史的経緯(HISTORICAL DEVELOPMENT)
(省略)
翼型の解説(DESCRIPTION OF AIRFOILS)
(省略)
理論上の考察(THEORETICAL CONSIDERATIONS)
(省略)
試験特性について(EXPERIMENTAL CHARACTERISTICS)
データの出自(SOURCE OF DATA)
試験データは主としてラングレイの二次元低乱流圧力風洞(TDT)によった。試験方法については巻末に記す。試験に用いられた翼弦長2フィートの翼型データについては付録図に示す。
ラングレイ以外の NACA 施設で計測された風洞データについては明記されている。特に注記がない限り、計測および補正方法は通常の(conventional)ものである。
飛行データの多くは後流観測法(wake-survey method)による。翼型は実機翼型あるいは実機翼に被せるグローブ(glove)による。グローブを用いたデータについては明記されている。高速で計測されたデータについては圧縮流法(compressive-flow method)を用いて定数化補正(reduced to cofficient form)されている。全ての飛行データについて、低エネルギー気流の流入(cross flows of low-energy air)による外乱を避ける配慮がなされている。
平滑翼型の抵抗特性(DRAG CHARACTERISTICS OF SMOOTH AIRFOILS)
低抵抗域の抵抗特性(Drag characteristics in low-drag range)
平滑翼型の低抵抗域における抗力係数は主としてレイノルズ数と相対的な層流範囲(extent of laminar flow)の関数となり、翼厚比とキャンバーによってもやや影響を受ける。層流範囲に決定的な影響を与えると考えられる最小圧力位置(position of minimum pressure)の変化と最小抗力係数の相関について、NACA 6- シリーズ翼型のデータを Figure.9 に示す。データは最小圧力位置の後退に伴って最小抗力係数が下がってゆく傾向を示している。
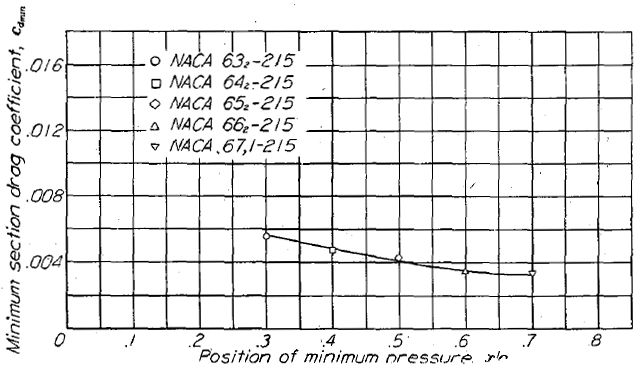 Figure.9 同じキャンバーと翼厚を持つ NACA6 シリーズ翼型の、最小圧力位置と最小抗力係数の相関。R=6x106.
Figure.9 同じキャンバーと翼厚を持つ NACA6 シリーズ翼型の、最小圧力位置と最小抗力係数の相関。R=6x106.
各種の翼型について、レイノルズ数と最小抗力係数の相関を Figure.10 に示す。全体的に、レイノルズ数が 20x106 までの領域ではレイノルズ数の増加に伴い抗力係数は下がっている。NACA 65(421)-420 の抗力係数は 40x106 までほぼ一定である。これに比して NACA 66(2x15)-116 の抗力係数が早期に増加しているのは、この翼型模型が実機製法(practical construction method)で製作されたことによる表面荒度によるものと思われる。
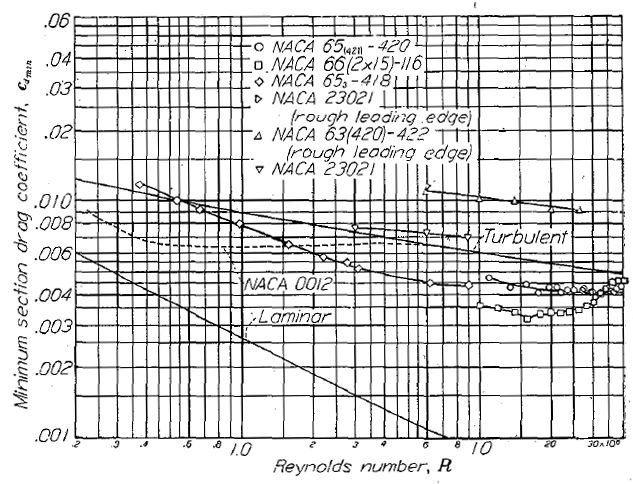 Figure.10 各種翼型におけるレイノルズ数と抗力係数の相関、平板における層流と乱流の摩擦抗力係数も共に示す。
Figure.10 各種翼型におけるレイノルズ数と抗力係数の相関、平板における層流と乱流の摩擦抗力係数も共に示す。
NACA 653-418 の抗力係数が小レイノルズ数域において NACA 0012 より著しく大きく、大レイノルズ数域においては逆転していることに注目されたい。小レイノルズ数域における 653-418 の大抵抗は、最小圧力位置後方の比較的大きな領域で層流が剥離している(relatively extensive region of laminar separation)ことによって発生している。レイノルズ数の増大に伴って剥離域は小さくなる。これらのテストデータは実機サイズの特性予測についても、あるいは飛行レイノルズ数域における翼型間の比較についても、小レイノルズ数域でのデータが不足していることを示している。(資料 25, 26)
翼厚比 18% の NACA 6- シリーズ翼型について、キャンバーと最小抗力係数の相関を Figure.11 に示す。キャンバーの増加に伴う抗力係数の変化はごくわずかである。
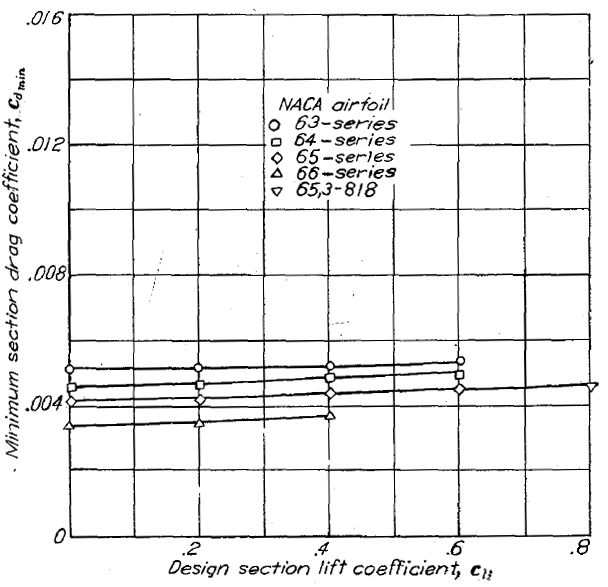 Figure.11 翼厚比 18% を持つ NACA 6- シリーズ翼型各種のキャンバーと最小抗力係数の相関。R=9x106.
Figure.11 翼厚比 18% を持つ NACA 6- シリーズ翼型各種のキャンバーと最小抗力係数の相関。R=9x106.
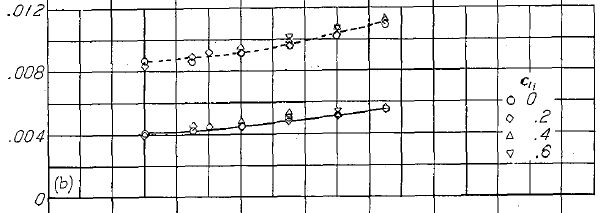
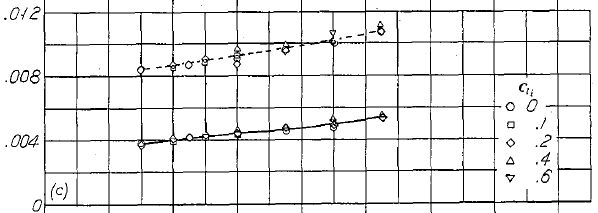
翼型、翼厚比と最小抗力係数の系統的な相関を Figure.12 に示す。全ての翼型について、翼厚増加に伴う抗力係数の増加が認められる。しかしながら、その増加率は NACA 4 および 5 桁の従来翼型(Figure.12(a))よりも、NACA 6- シリーズ翼型(Figure.12(b)〜(e))のほうが小さい。
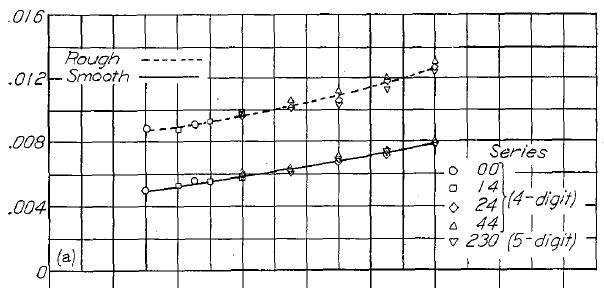
 (a) NACA 4 桁および 5 桁
(a) NACA 4 桁および 5 桁
(b) NACA 63- シリーズ
(c) NACA 64- シリーズ
(d) NACA 65- シリーズ
(e) NACA 66- シリーズ
Figure.12 各種 NACA 翼型の、平滑と前縁荒面ありの場合の翼厚比と最小抗力係数の相関。R=6x106.
NACA 6- シリーズの翼厚変化に関する付録図が示すように、低抵抗域における揚力係数は明らかに翼厚比によって変化する。翼厚比 12% ならば低抵抗域における揚力係数 0.2 の翼型を設計することが可能である。理論上は翼厚比 3% の増加あたり揚力係数約 0.2 の割合で相関する。Figure.13 はレイノルズ数 9x106 において、理論上の低抵抗域が実際に観測されることを示している。Figure.13 はまた、中程度のキャンバーを持つ翼型が低抵抗域の上端において抗力係数が増加する特性を示しており、これは翼厚比の厚い翼型について特に顕著である。
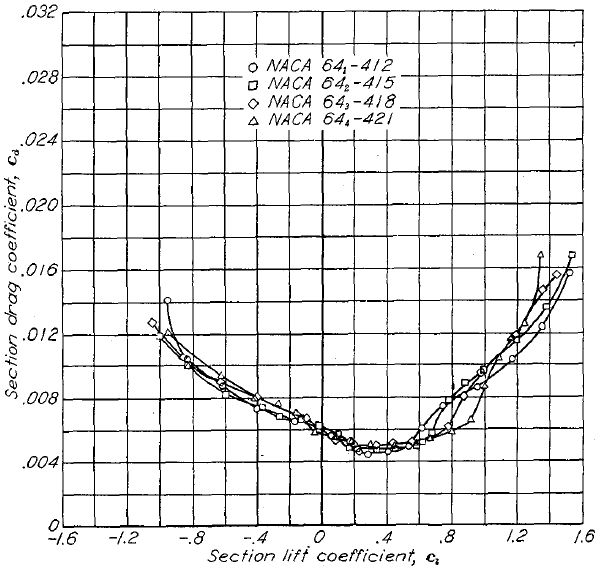 Figure.13 設計揚力係数 0.4 のキャンバーを与えた翼厚比数種の NACA 64- シリーズ翼型の揚力特性。R=9x106; TDT tests 082, 733, 735 and 691.
Figure.13 設計揚力係数 0.4 のキャンバーを与えた翼厚比数種の NACA 64- シリーズ翼型の揚力特性。R=9x106; TDT tests 082, 733, 735 and 691.
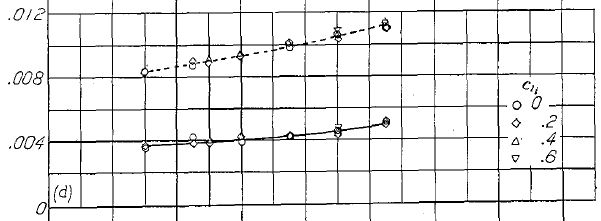
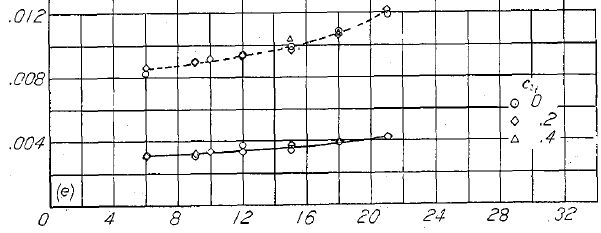
全ての NACA 6- シリーズ翼型は、レイノルズ数の増大に伴って低抵抗域が縮小する。レイノルズ数 9x106 以下での減少傾向から推定すると、飛行レイノルズ数域での低抵抗域は皆無に近いほど狭くなると予想される。しかしながら、注意深く製作された NACA 65(421)-420 翼型模型を用いた実験では、レイノルズ数 9x106 以上において、レイノルズ数増大に伴う低抵抗域の縮小傾向は大幅に減少することを示している(Figure.14)。これらの実験データは、この翼型において、レイノルズ数 35x106 での低抵抗域幅は理論値の約半分になることを示している。
 |
 |
(a) 上面と下面におけるレイノルズ数と低抵抗域限界の相関.
|
(b) レイノルズ数と抵抗特性の相関。 |
Figure.14 NACA 65(421)-420 翼型におけるレイノルズ数と低抵抗域の相関。TDT tests 300, 312 and 328.
図をクリックすると別ウィンドウに拡大表示
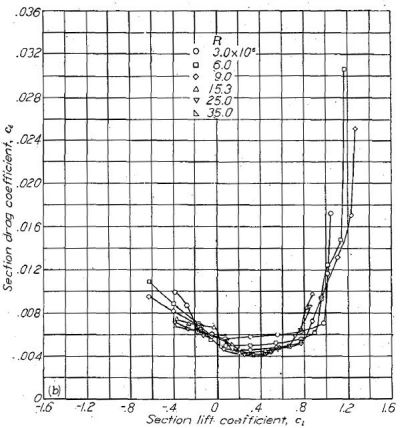
低抵抗域での揚力係数はキャンバーによって支配的な影響を受ける。低抵抗域中央での揚力係数はおおむね基準線(mean line)における設計揚力係数に一致する。各種キャンバーと抵抗特性の相関を Figure.15 に示す。翼型データが示すキャンバーの変化と低抵抗域の移動の相関は、フラップのわずかな下げによってもこのような変化が生じることを示唆する。
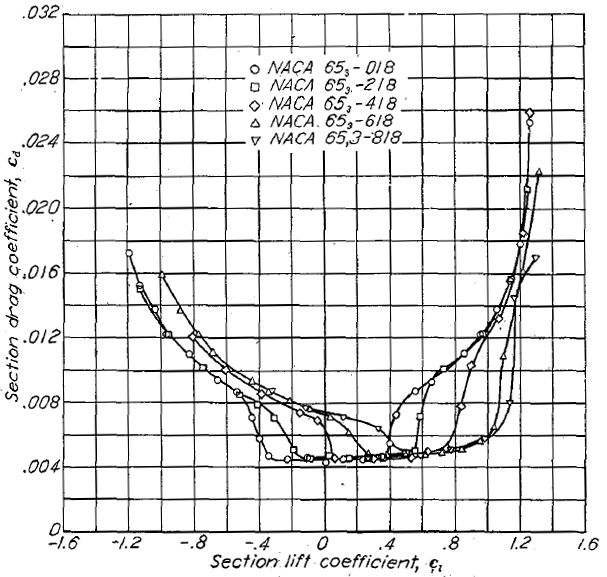 Figure.15 翼厚比 18% の NACA 65- 翼型におけるキャンバーと抵抗特性。R=6x106; TDT tests 163, 314, 802, 813 and 830.
Figure.15 翼厚比 18% の NACA 65- 翼型におけるキャンバーと抵抗特性。R=6x106; TDT tests 163, 314, 802, 813 and 830.
低抵抗域の位置は、単純な薄翼理論から予測される変異を示している。この揺らぎは翼型設計に用いられた基準線(資料 27)と翼厚に由来するものと考えられる。低抵抗域の移動要因の一部は、前章で解説したように、設計揚力係数よりも高い揚力域での速度分布が変化することによっても説明される。
低抵抗域外での抵抗特性(Drag characteristics outside low-drag range)
低抵抗域の終端では、揚力係数の増加に合わせて急激に抵抗が増大している。低抵抗域終端近くでの揚力係数がそれほど高くない対称翼および中程度キャンバーの翼型では、この抵抗の増大は持続しない(Figure.15)。キャンバーの強い翼型では低抵抗域終端近くで揚力係数は既に高まっており、急激な抗力係数の増加も持続する。均等荷重基準線(uniform load mean line)に合わせたキャンバーを与えた翼型と、より前方に荷重を寄せたキャンバーの比較では、均等荷重分布のほうが大揚力域でより好ましい低抗力係数を示している(Figure.16 および資料 27)。
付録図で示したように、多くの翼型では大揚力域において、レイノルズ数の増大に伴って抵抗が低下している。このスケール効果は表面摩擦の変異だけでは説明できず、前縁近くで層流から乱流に遷移した後のレイノルズ数の効果によるものと考えられる(資料 28)。
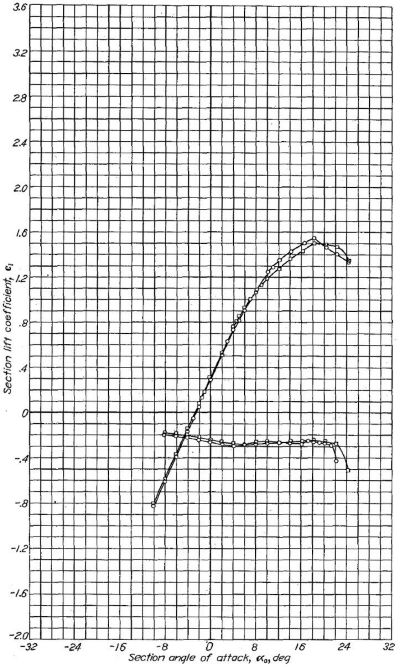
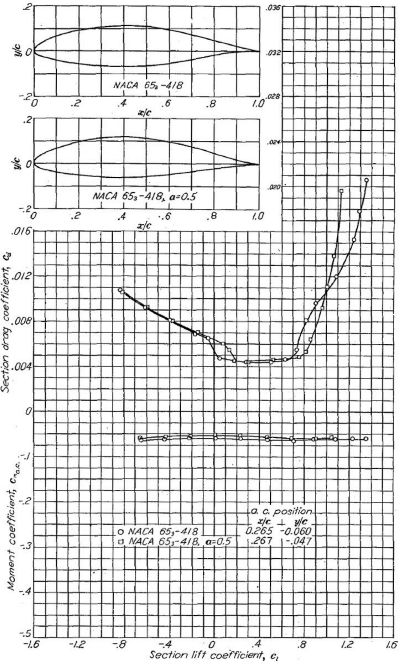
Figure.16 レイノルズ数 9x106におけるNACA 653-418 と NACA 653-418 α=0.5 翼型の比較。TDT tests 314, 320, 406 and 411.
図をクリックすると別ウィンドウに拡大表示
翼型と抵抗の特性(Effects of type of section on drag characteristics)
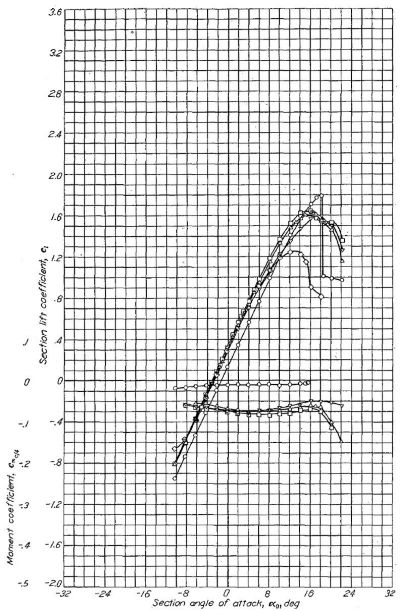
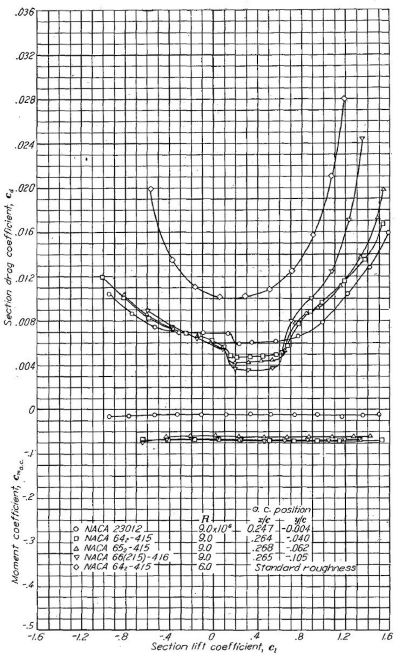
NACA 23012 と NACA 6- シリーズの比較を Figure.17 に示す。高速飛行で用いられる揚力域において、NACA 6- シリーズは NACA 23012 に比して大幅に低い抵抗を示しており、この特性は適切なキャンバーの選択により巡航速度域にまで拡大できると思われる。NACA 6 シリーズの最大揚抗比はより高い値を示しているが、大揚力係数域においては、従来翼型のほうが NACA 6- シリーズより低い抗力係数を示している。
Figure.17 ラングレイの二次元低乱流圧力風洞における NACA 翼型数種の空力特性比較。
図をクリックすると別ウィンドウに拡大表示
有効アスペクト比(Effective aspect ratio)
NACA 6- シリーズの高揚力係数域における大抵抗、中揚力係数域における低抵抗、揚抗比の非線形的な特性という組み合わせは、飛行機の性能推算に用いられる翼幅効率原理(資料 29)に矛盾を投げかける。この原理は通常、飛行機の抵抗を下記の関数で近時して考える。
CD=C
DL=0+kC
L2 式 (17)
この関数は通常、低〜中程度の揚力係数域において実測された抵抗特性によく一致する(資料 30)。
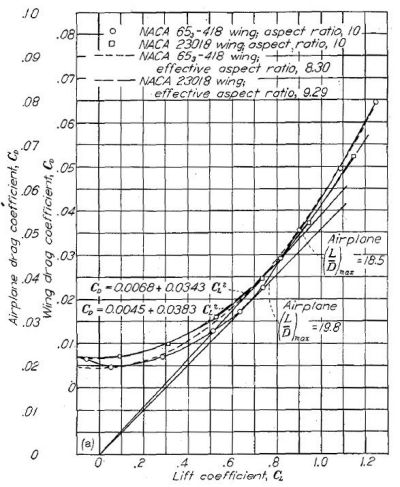
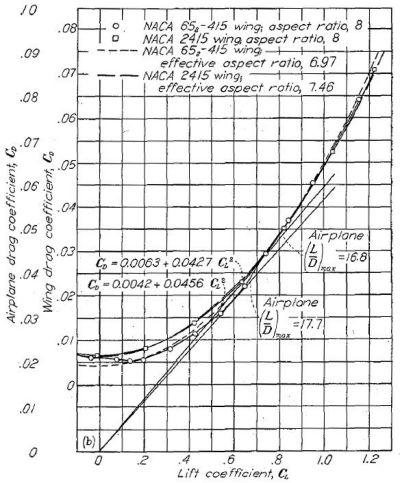
NACA 230- および NACA 65- 翼型を用いた仮想航空機にこの原理を適用した試算結果を Figure.18(a) に示す。主翼抵抗にはアスペクト比 10、楕円分布の誘導抵抗が NACA 23018 および NACA 65
3-418 翼型の有害抵抗に上乗せされている。これらの翼型はこのアスペクト比を持つ大型航空機の代表として考えている。Figure.18(a) の縦軸は主翼抗力係数および、0.0150 の固定値を加算した全機抗力係数である。算出された2本の曲線は式 (17)に近似し、揚力係数 0.2 および 1.0 において抵抗カーブに一致する。NACA 23018 のアスペクト比 9.29、NACA 65
3-418 のアスペクト比 8.30 を持つ仮想航空機の2本の曲線は、このような翼型における有効アスペクト比の大きな減少を示している。
注目すべきは、式(17)は NACA 23018 の仮想航空機について満足できる近似結果を示しているのに対し、NACA 65
3-418 の仮想航空機については必ずしも当てはまらないことである。大型機が大アスペクト比を用いる最も重要な理由は巡航揚力域における抵抗を削減し、揚坑比を最大にすることである。2種の仮想航空機を比較すると、NACA 65
3-418 を用いた機体のほうが揚坑比が高い(18.5 に対し 19.8)が、有効アスペクト比は低い。Figure.18(b) はアスペクト比 8 で NACA 2415 と 65
2-415 を比較したものだが、同様の結果を示している。これらの試算結果は、有効アスペクト比が翼型選定の評価基準として不十分であることを結論づける。
 |
 |
(a) アスペクト比 10 の NACA 653-418 および 23018 の翼.
|
(b) アスペクト比 8 の NACA 652-415 および 2415 の翼.
|
Figure.18 有限アスペクト比を持つ翼における2種類の翼型主翼に楕円分布の誘導抵抗を加味した比較。
図をクリックすると別ウィンドウに拡大表示
許容可能な表面荒度(Permissive roughness)
以前からの実験により、表面荒度は大幅な抵抗の増大をもたらすことが知られている(資料 31)。この抵抗増大の大部分は遷移点の前進がもたらすものであるが、少なくない抵抗が乱流遷移後の表面荒度によっても増大している。すなわち、広範囲な層流の維持が期待できない場合でも表面の平滑さを保つことは重要なのであるが、NACA 6- および 7- シリーズの層流翼型では、表面を平滑にして広範囲な層流の維持ができた場合に得られる利益は一層大きなものとなる。
大レイノルズ数域における表面状態を記述する正確な手法は確立されていないが、一般的な結論は得られている。レイノルズ数と翼弦位置が与えられたならば、許容可能な表面荒度の大きさは翼弦に直接相関する。極論するならば、表面は鏡面のように磨き上げる必要はない。ラングレイの二次元低乱流風洞を用いた実験によれば、そのような研磨やワックス仕上げは、満足すべきサンドペーパー仕上げに対して向上を示さない。もちろん空力的に平滑ではない表面に対する研磨やワックス仕上げは効果があるし、そのような仕上げの劣化は目視で容易に確認できるため、実用的な価値もあるであろう。ラングレイの二次元風洞における翼弦長 5〜8 フィートの大型翼型模型の場合、空力的に平滑な仕上げが必要な場合、表面を 320 番のサンドペーパーで翼弦方向に研磨した。経験的に、この仕上げは飛行レイノルズ数域において満足すべき結果を示す。これより荒い表面は遷移の発生を促すと考えられるが、場合によっては多少荒い程度の仕上げでも満足すべき結果を得ることもある。
NACA 6- シリーズ翼型の風洞実験によれば、磨かれた表面上への突出物は、凹む場合よりも遷移源になる。例えば、粉塵は引っかき傷よりも(傷の縁部が突出しないかぎり)効率的に遷移を引き起こす。大レイノルズ数域においては、油に汚れた手で触った指紋跡に付着した粉塵でも遷移を引き起こすと考えられる。
乱流源による遷移は約 15 度の角度をもって下流に広がる(資料 31, 33)。分散した突出物であっても、特にそれが主翼前縁に近ければ広範囲な乱流を引き起こす。これはすなわち、低抵抗が求められる場合、非常に慎重な平滑検査が必要であることを意味する。実機サイズの翼型で遷移を引き起こすような突出物は手で触れて感じることができる。ラングレイの二次元低乱流圧力風洞では、翼型模型を素手で撫でて検査し、引っ掛かりを感じた場合は乾いた布で磨くという検査手順が取られた。
突出物による遷移の発生は外板波打ちとは異なり、突出点の直後から発生する。外板波打ちによる遷移はより下流で発生し、波打ちの大きさおよびレイノルズ数に応じて波打ち点に近づいてくる。Figure.19 は翼弦 5% に置いた円柱状の突出物が乱流遷移を引き起こす高さとレイノルズ数の相関である。このデータは比較的小さなレイノルズ数域で取得されているが、レイノルズ数の増大に伴って許容高さが急速に小さくなってゆく傾向を示している。このレイノルズ数との相関は Figure.20 において、迷彩ラッカー塗装仕上げがレイノルズ数 20x106 付近で抵抗急増しているデータとも符合する。
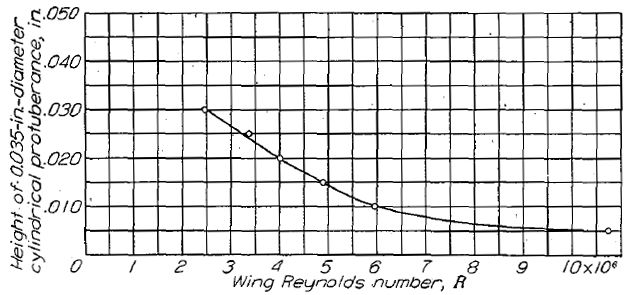 Figure.19 レイノルズ数と乱流遷移限界の円柱突起高さの相関。突起は 0.035 インチ直径で翼面に対し垂直に、翼弦長 90 インチ翼厚比 15% 最小圧力位置翼弦 70% の 6- シリーズ翼型模型の翼弦前縁 5% に置いた。
Figure.19 レイノルズ数と乱流遷移限界の円柱突起高さの相関。突起は 0.035 インチ直径で翼面に対し垂直に、翼弦長 90 インチ翼厚比 15% 最小圧力位置翼弦 70% の 6- シリーズ翼型模型の翼弦前縁 5% に置いた。
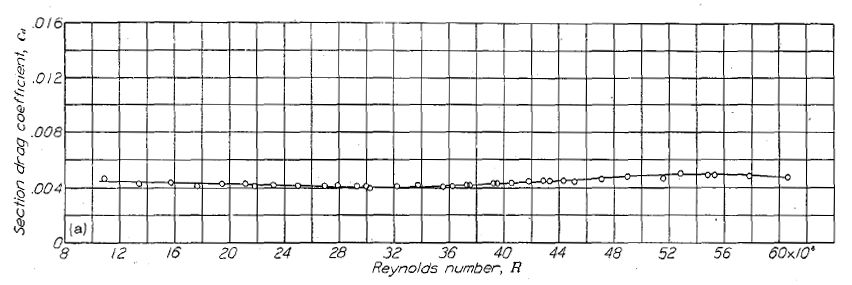
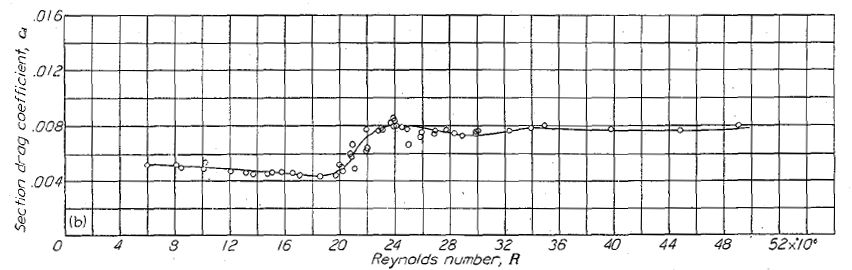 (a) 平滑表面; TDT test 328.
(a) 平滑表面; TDT test 328.
(b) ラッカー迷彩塗装の塗布後再仕上げなし; TDT test 461.
Figure.20 2種類の表面状態における翼弦長 60 インチの NACA 65(421)-420 翼型模型におけるレイノルズ数と抗力係数の相関。
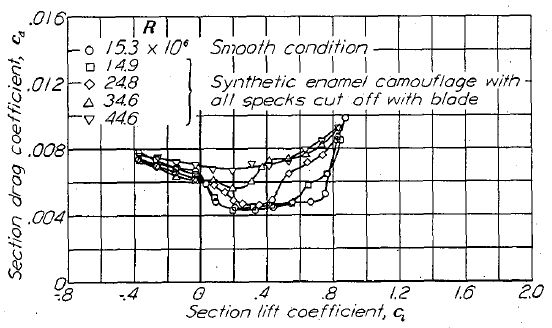 Figure.21 2種類の表面状態における NACA 65(421)-420 翼型の抵抗特性。TDT tests 300 and 486.
Figure.21 2種類の表面状態における NACA 65(421)-420 翼型の抵抗特性。TDT tests 300 and 486.
好ましい圧力勾配(favorable pressure gradient)が層流にもたらす効果は表面荒度よりも小さい。Figure.21 に示したデータは、表面荒度が低抵抗域の右端でより重要な影響をもたらすことを示しているが、この領域では好ましい圧力勾配は片面だけにしか発生していない。中程度の荒さの場合、レイノルズ数を大きくすることは、一定のレイノルズ数下において荒さを大きくしてゆくのと同じような挙動を見せ、これは低抵抗域の縮小と最小抗力係数の増加をもたらす(Figure.21)。Figure.21 のデータはこの効果を示すため特に選択されたものである。ほとんどの場合、好ましい圧力勾配の減少が低抵抗域の消失を示すだけなのに対し、レイノルズ数は抗力に対してより支配的な影響をもたらす。
許容可能な表面の波打ち(Permissive waviness)
層流を維持するためには、表面の平滑さよりも波打ちを減らすことのほうが困難である。これに加えて、波打ちの許容度を定量的に表記することは平滑さよりも難しい。層流に影響を与える波打ちの最小値を求めるだけでは済まず、波の数や形状も考慮しなければならないからである。波打ちが圧力分布に影響を与えて層流剥離をもたらすほど大きな場合、有用レイノルズ数域において遷移の促進をもたらすことは疑う余地もない。圧力分布と波打ちの大きさの相関については資料 35 で述べられている手法が有用であろう。好ましい圧力勾配の逆転をもたらす波の大きさは、圧力勾配の増加に応じて大きくなる。すなわち、波打った翼面においては大きな負の圧力勾配が好ましいことになる。実験はこの仮説が有意に正しいことを裏付けている。
層流剥離や圧力勾配逆転を引き起こすには小さすぎるほどの波打ちの影響については情報が少ない。上面に比較的長い波打ちを持つ翼型のデータを Figure.22 に示す。遷移点の前進と抵抗の増加はレイノルズ数 44x106 に至るまで顕著には現われない。しかしながら、翼弦 60 インチの翼型において長さ 2 インチ・高さ数千分の 1 インチの複数の波打ちが、比較的小さなレイノルズ数域において遷移を起こしたこともあった。
実機製法による翼型の波打ちの検出には、直線定規(straightedge)を翼面に当て翼弦方向に回転させる評価法がある。定規が引っかかりなくスムーズに動くなら翼面状態は良好と考えられる。この手法では Figure.22 のような凹みは検出できないが、多くの実機製法翼型模型による実験の結果、直線定規による検査をパスした翼型は実用的に充分な仕上げ精度を持ち、飛行レイノルズ数域において低抵抗を示す。
工作精度や翼型との一致精度を定量的に指定することは現実的ではない。表面仕上げに充分な注意が払われるならば、通常の工作精度指定において抵抗特性に大きな影響を与えない翼が実現できるであろう。
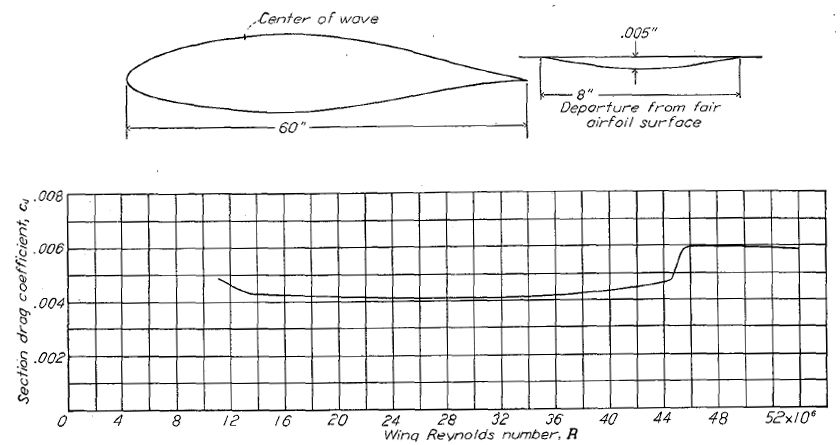 Figure.22 前縁に僅かな波打ちのある NACA 65(421)-420 横型における抗力係数変化の実験結果。
Figure.22 前縁に僅かな波打ちのある NACA 65(421)-420 横型における抗力係数変化の実験結果。
固定遷移による抵抗(Drag with fixed transition)
主翼表面が前縁近くで遷移を起こすほどに荒い場合、大きな抵抗の増加が予想される。荒さの程度は抵抗に多少の影響を与えはするが、Figure.23 は小さな遷移源であっても翼前縁で起きる限り、より大きな粒と同程度の遷移を引き起こすことを示している。荒さの影響は大揚力係数域においてより顕著となる。全レイノルズ数域において遷移が起きるほど大きな荒さが翼前縁のみにある場合、抵抗はレイノルズ数の増大のみによって減少する(Figure.10 および資料 36)。
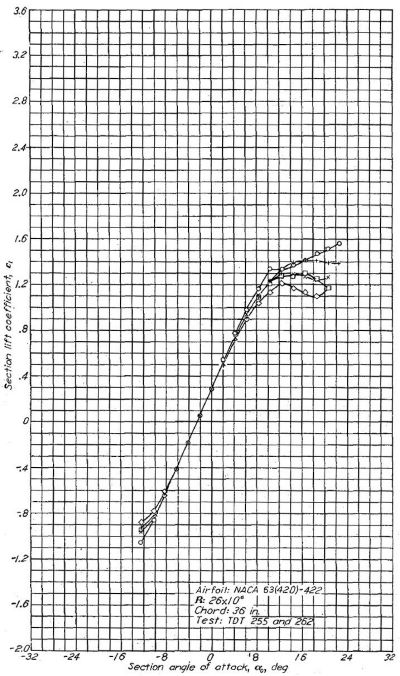
Figure.23 NACA 63(420)-422 翼型における、各種前縁状態の揚力抵抗特性。
図をクリックすると別ウィンドウに拡大表示
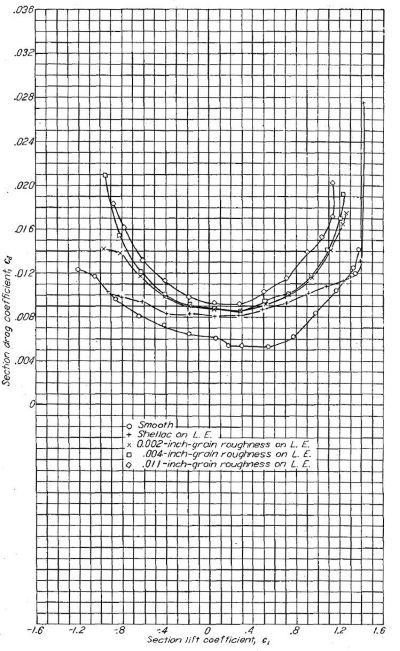
0.011in 直径の炭化珪素粒からなる荒面帯(roughness strip of carborundum of 0.011-inch grain)による固定遷移の影響を Figure.24 に示す。最小抵抗は荒面帯の前進と共に次第に増大する。大揚力係数における抵抗増大は漸次的ではなく、荒面帯が最前縁にある場合に急増する。
Figure.24 NACA 63(420)-422 翼型における、0.011 インチ粒の翼弦位置と揚力抵抗特性。
図をクリックすると別ウィンドウに拡大表示
Figure.25 は層流が前縁 30% に限定される場合、 NACA 65(223)-422 および 63(420)-422 翼型の抗力係数が殆どの揚力域において概ね同等であることを示している。
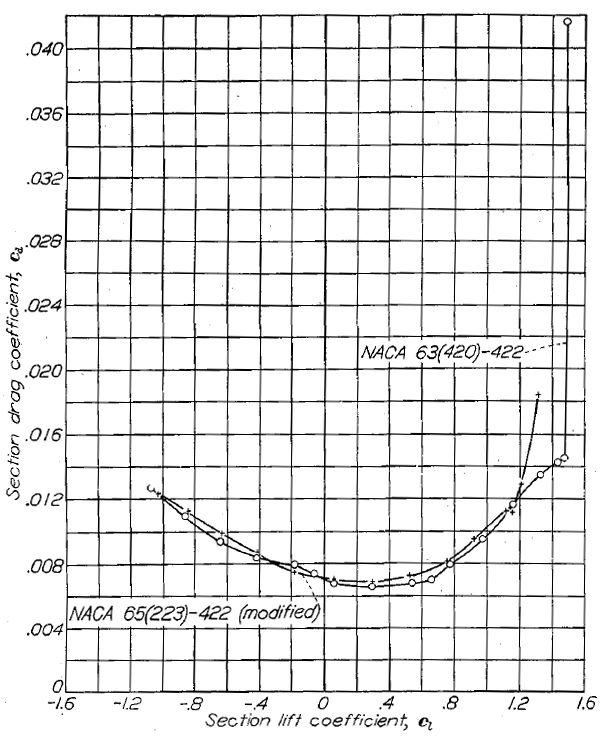 Figure.25 前縁 30% に 0.011 粒の荒面帯を置いた NACA 6- シリーズ翼型2種の抵抗特性。R=26x106.
Figure.25 前縁 30% に 0.011 粒の荒面帯を置いた NACA 6- シリーズ翼型2種の抵抗特性。R=26x106.
ラングレイの二次元低乱流圧力風洞によって計測された、前縁を荒らした置いた場合も含めた翼型のデータを付録図に示す。以前は前縁を荒らした場合のデータ測定は翼厚比の大きな一部の翼型に限られていた(資料 37)。24 インチ翼弦の翼型模型における「標準荒度(standard roughness)」は 0.011in 直径の炭化珪素粒を翼弦 0.08% の幅にわたって塗布したものである。粒は 5〜10% の密度で薄く均等に塗布される。この「標準荒度」は一般的な実機製法によって生じる工作荒れ、あるいは整備によって発生する荒れよりは大きく、しかし実戦機が前線で遭遇する氷や泥の付着、あるいは戦闘による破損よりは小さいと考えられる。
Figure.12 は各種の NACA 翼型に対し、標準荒面帯(standard roughness strip)の有無と翼厚比による抗力係数の相関を示したものである。このデータは NACA 6- シリーズの最小抗力係数は 4 桁および 5 桁シリーズより小さいことを示している。翼厚比増大に伴う抵抗の増加は、表面が平滑よりも粗いほうが大きくなる。
実機製法に伴う抵抗(Drag with practical construction method)
何種かの翼型の抗力係数は実機飛行および後流観測法によって測定され(資料 38)、また何種かの実機製法翼型模型がラングレイの二次元低乱流圧力風洞において飛行レイノルズ数域でテストされた。NACA による飛行実験(資料 38)を Figure.26 に、またコンソリデーテッド・バルティ社によるデータを Figure.27 に示す。ラングレイの二次元低乱流圧力風洞において計測された実機製法翼型模型のデータを Figure.28〜32 に示す。Figure.33 は NACA0012 翼型模型の風洞と実機に取り付けた飛行条件での抵抗を示す。この場合、風洞のデータと実機飛行条件のデータは誤差範囲内でよく一致している。
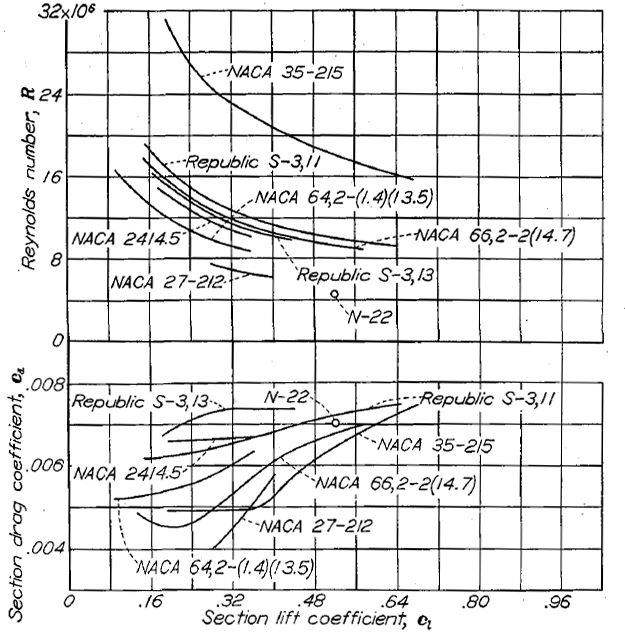 Figure.26 飛行実験によって得られた翼型の抗力係数比較。NACA 27-212 と 35-215 はグローブによる測定。
Figure.26 飛行実験によって得られた翼型の抗力係数比較。NACA 27-212 と 35-215 はグローブによる測定。
Figure.26 に示された、飛行条件で測定された全ての翼型模型は平滑な表面状態を実現するよう注意深く仕上げられている。NACA 2414.5、N-22, Republic S-3,13, NACA27-212 を除き、表面の波打ちを最小限にするよう最大限の注意が払われている。Figure.27 における表面状態については図中に示される。これらのデータは、広範な層流が実現できる平滑な表面の翼型の場合、他の翼型よりも著しく抗力係数が低くなることを示している。
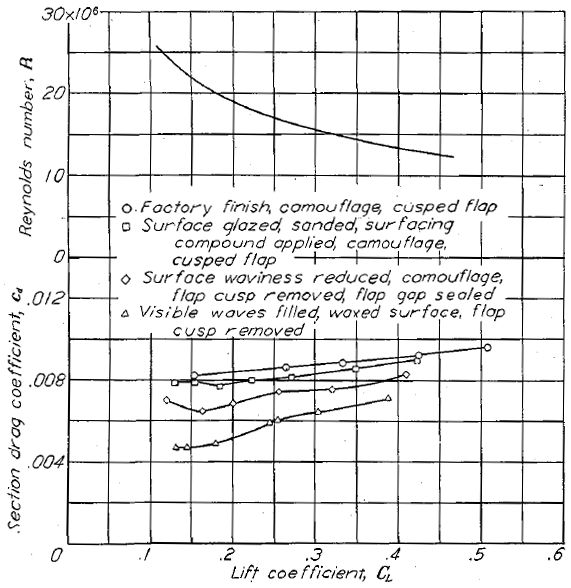 Figure.27 コンソリデーテッド・ヴァルティ社による NACA 66(215)-1(14.5)翼型に対する表面状態の影響測定。
Figure.27 コンソリデーテッド・ヴァルティ社による NACA 66(215)-1(14.5)翼型に対する表面状態の影響測定。
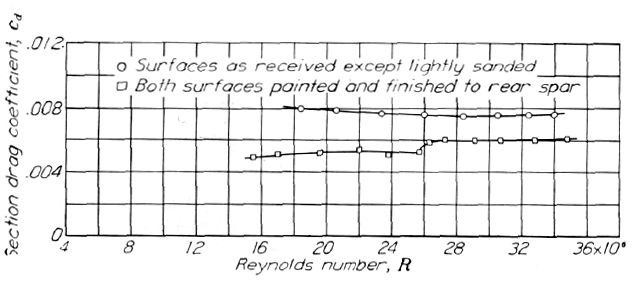 Figure.28 実機製法で作られた翼弦長 100 インチの NACA 65(216)-3(16.5) (約)翼型における抵抗のスケール効果。CL=約 0.2.
Figure.28 実機製法で作られた翼弦長 100 インチの NACA 65(216)-3(16.5) (約)翼型における抵抗のスケール効果。CL=約 0.2.
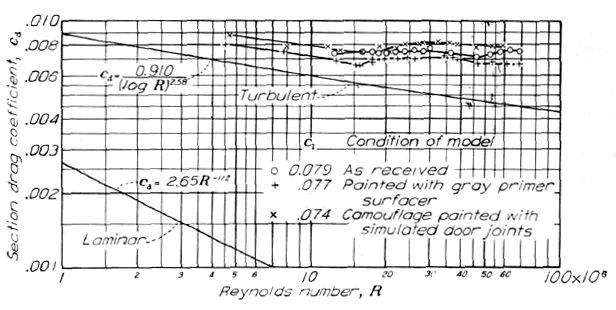 Figure.29 NACA 23016 翼型の表面仕上げと抗力係数の相関。平板における層流と乱流の摩擦抗力係数も共に示す。
Figure.29 NACA 23016 翼型の表面仕上げと抗力係数の相関。平板における層流と乱流の摩擦抗力係数も共に示す。
航空機メーカーから納品された実機製法翼型は、採用した翼型に関わらず最小抵抗係数 0.0070〜0.0080 を示していた(Figure 28〜32)。現在の航空機製法において、これは良好な仕上げだと考えられる。翼面の平滑化は常に大幅な抵抗係数の減少を見せたが、ある程度の外板の波打ちは残った。試験に用いられた翼型模型のいずれも外板と前桁の結合部は平滑ではなかった。特別な措置が取られない限り、この波打ちは前桁部あるいはその直後から乱流遷移を発生させる。試験翼型のひとつ、Figure.10 の NACA 66(2x15)-116 はレイノルズ数 30x106 に至るまで良好な低抵抗特性を示した。この模型は翼弦 35% から先に桁を持たず、桁から前方には翼幅方向の強度材も持っていない。この構造によって非常に平滑な表面が実現でき、最新の高性能機にはこのような構造が採用されつつある。
実機製法模型において、翼型と抵抗係数の相関を正確に測定することは難しい。往々にして表面仕上げの差が翼型差以上の影響をもたらすからである。現実的なのは同一メーカーによって同時期に作られた別翼型模型を比較することであろう。Figure.30〜32 はそのようなペアの比較データである。これらのデータが示すのは、現在の航空機製法が取られる限り、軍用機が常用するレイノルズ数域において翼型の違いは比較的小さな効果しか示さないであろう、ということである。
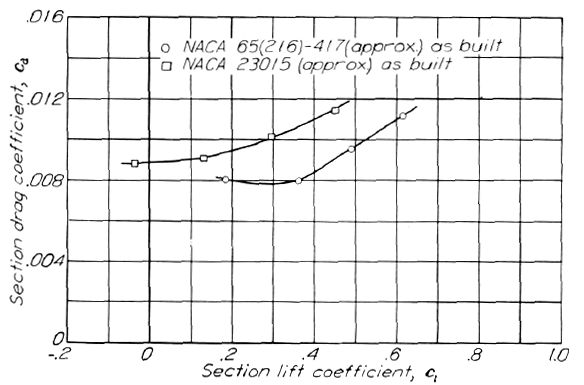 Figure.30 同一製造元によって実機製法で製作された NACA 65(216)-417(約) 翼型と NACA 23015(約) 翼型の抵抗特性。R=10.23x106.
Figure.30 同一製造元によって実機製法で製作された NACA 65(216)-417(約) 翼型と NACA 23015(約) 翼型の抵抗特性。R=10.23x106.
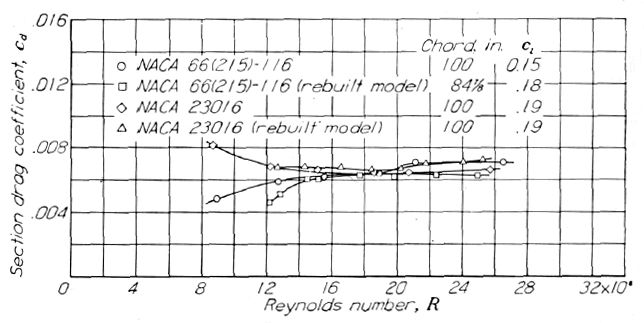 Figure.31 同一製造元によって実機製法で製作された、製造時状態における NACA 65(215)-116 翼型と NACA 23016 翼型の抗力スケール効果。
Figure.31 同一製造元によって実機製法で製作された、製造時状態における NACA 65(215)-116 翼型と NACA 23016 翼型の抗力スケール効果。
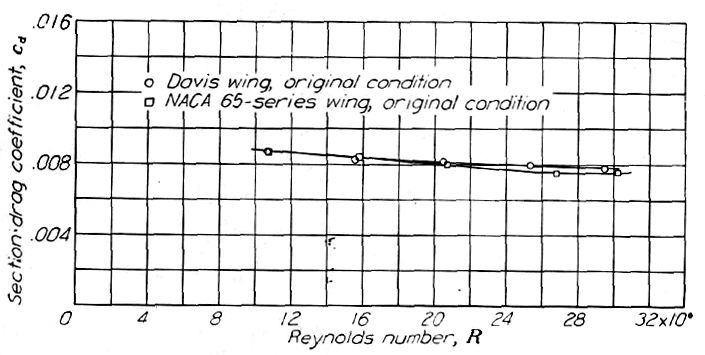 Figure.32 同一製造元によって実機製法で製作された、翼厚比 18.27% の NACA 65- シリーズ翼型と 18.27% デイビス翼型における抗力スケール効果。CL=約 0.46.
Figure.32 同一製造元によって実機製法で製作された、翼厚比 18.27% の NACA 65- シリーズ翼型と 18.27% デイビス翼型における抗力スケール効果。CL=約 0.46.
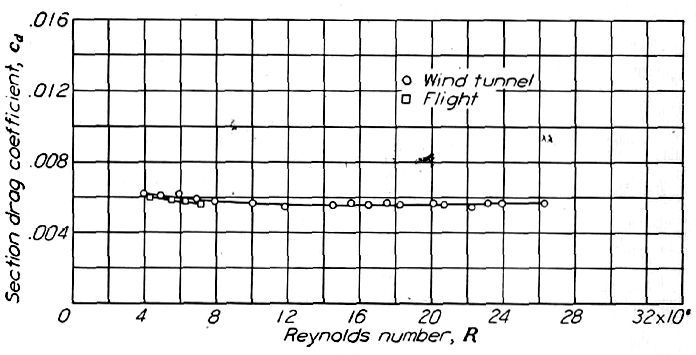 Figure.33 NACA 0012 翼型のゼロ揚力状態における抗力係数の、風洞実験と飛行実験の比較。
Figure.33 NACA 0012 翼型のゼロ揚力状態における抗力係数の、風洞実験と飛行実験の比較。
大レイノルズ域においては、たとえ層流が実現できなくとも、表面の平滑化によって重要な抵抗の削減が得られる。乱流域においても表面荒度によって抗力が増大するとが知られている(資料 31)。表面荒度がもたらす抗力とレイノルズ数の相関を Figure.29 に示すが、ここでは通常大レイノルズ数域で期待できるスケール効果が現われていないことに注目されたい。このようなスケール効果は Figure.10 における、前縁部のみに乱流源を置いた 63(420)-422 と比較されるべきであろう。飛行状態における固定遷移から発生する境界層の乱流化と抵抗の増大については資料 39 に示した。
平滑な翼型2種に対する、前縁への防氷装置の装着による影響を Figure.34 に示す。どちらも防氷ブーツは製造メーカーによって現実的に良好と考えられる状態で装着されている。防氷ブーツ装着時の最小抗力係数はどちらの翼型でも大レイノルズ数域において 0.0070 前後である。
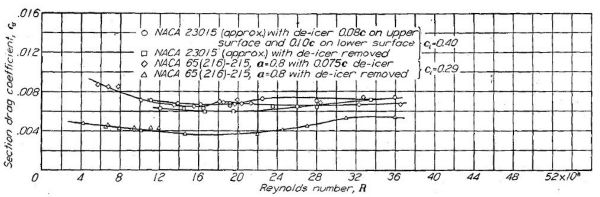 Figure.34 実機製法で製作された、比較的平滑な表面仕上げの翼型2種に対する防氷装置の影響。
Figure.34 実機製法で製作された、比較的平滑な表面仕上げの翼型2種に対する防氷装置の影響。
図をクリックすると別ウィンドウに拡大表示
プロペラ後流と震動の影響(Effects of propeller slipstream and airplane vibration)
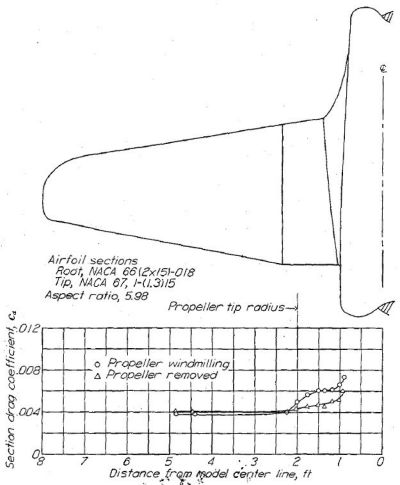
プロペラ後流と遷移の相関を示したデータは少なく、限られたデータも一定の傾向を示すとは限らない。この不定性は揚力係数、表面状態、気流状態、プロペラの捻り比、プロペラ枚数などの条件の違いに起因するものと思われる。ラングレイの 8 フィート高速風洞による実験では、翼弦の 5〜10% で遷移が発生する(資料 40)。ラングレイの 19 フィート圧力風洞による抵抗の測定(Figure.35)では、空転するプロペラによる抵抗増大は中程度でしかない。プロペラ後流中では後流観測法の適用が困難であることから Figure.35 の精度は高くないと考えられるものの、このデータは遷移点が前縁に前進することによる非常に大きな抗力の増大は除外できると考えられる。このデータは NACA による実機飛行データ(Figure.36)によっても裏付けられる。このデータではプロペラ後流中でも遷移点は翼弦 20% 程度までしか前進していない。他の未公表の NACA 飛行データでは、プロペラ後流中の S-3,14.6 翼型において翼弦 20% 程度まで層流が発生したことを示している。
 |
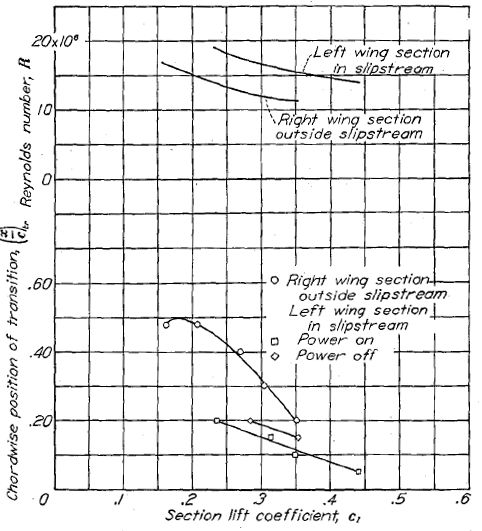 |
Figure.35 ラングレイ 19 フィート圧力風洞における戦闘機型航空機模型の
プロペラと翼型抗力係数の相関。CL=0.10; R=3.7x106.
図をクリックすると別ウィンドウに拡大表示 |
Figure.36 飛行状態における NACA 66- シリーズ翼のプロペラ後流内と外での遷移の測定。 |
震動については更にデータが少ない。ラングレイの 8 フィート高速風洞でのテスト(資料 40)では有意な影響が見られなかったが、この実験での震動は実機状態を再現するに充分な幅を持たなかったかも知れない。未公表データの一部には、プロペラをフェザーしたときにプロペラ後流外で小さな、しかし一定の遷移点の後退を示している。この効果は試験翼型の反対舷のプロペラをフェザーした時にも現われたため、プロペラ後流ではなく震動によるものと考えられる。エイムスの実機大風洞を用いた最近の実験では、試験機を支える支柱を震動させた場合、抗力係数の逆スケール効果が早い段階で起こることが後流観測法によって観測されている。
平滑翼型の揚力特性(LIFT CHARACTERISTICS OF SMOOTH AIRFOILS)
二次元データ(Two-dimentional data)
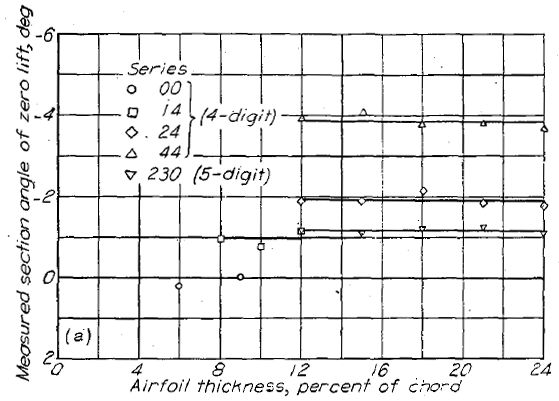
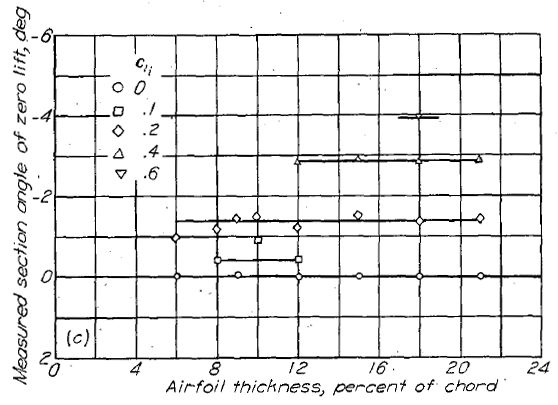
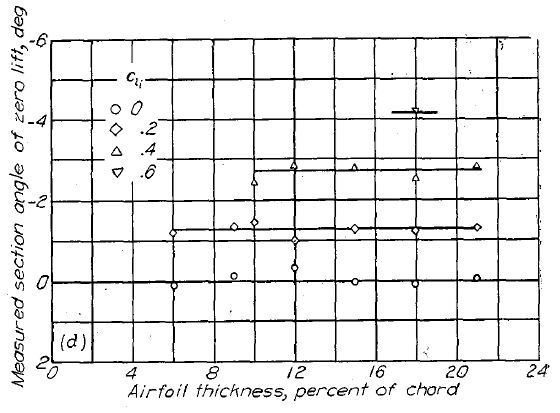
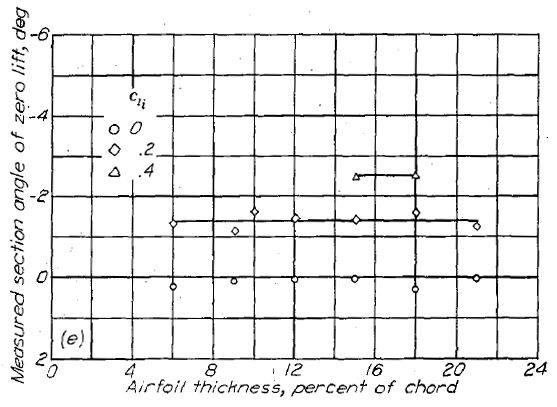
「ゼロ揚力角度」の項で解説したように、翼型のゼロ揚力角度は主にキャンバーによって決定される。薄翼理論は付録図に示される基準線(mean-line)からゼロ揚力角度を算出する式を与える。理論上のゼロ揚力角度と実験による角度の一致は使われる基準線の種類によって異なる。実験値と理論値を比較すると、両者はα=1.0の均等荷重(uniform-load type)の基準線を除けばよく一致している。このタイプの基準線のゼロ揚力角度は、予想されるよりも大きく正の値を取る。Figure.37 に NACA 4 桁、5 桁、6- シリーズ翼型各種のゼロ揚力角度を示す。翼厚比はゼロ揚力角度に大きな影響を与えないことが見て取れる。NACA 4 桁翼型の場合、ゼロ揚力角度は薄翼理論値の約 0.93 倍であり、230- シリーズでは約 1.08 倍、6- シリーズの均等荷重基準線では約 0.74 倍である。
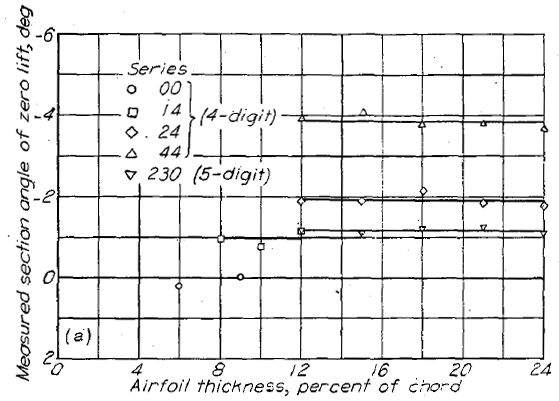 (a) NACA 4 および 5 桁 (a) NACA 4 および 5 桁 |
 (b) NACA 63- シリーズ (b) NACA 63- シリーズ |
 (c) NACA 64- シリーズ (c) NACA 64- シリーズ |
 (d) NACA 65- シリーズ (d) NACA 65- シリーズ |
 (e) NACA 66- シリーズ (e) NACA 66- シリーズ |
|
Figure.37 各種 NACA 翼型の翼厚・キャンバーとゼロ揚力角度の相関。R=6x106.
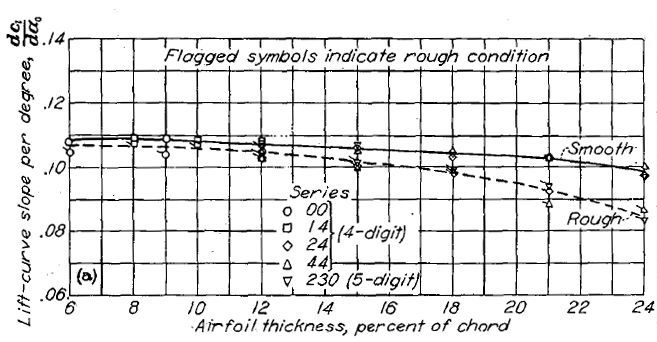
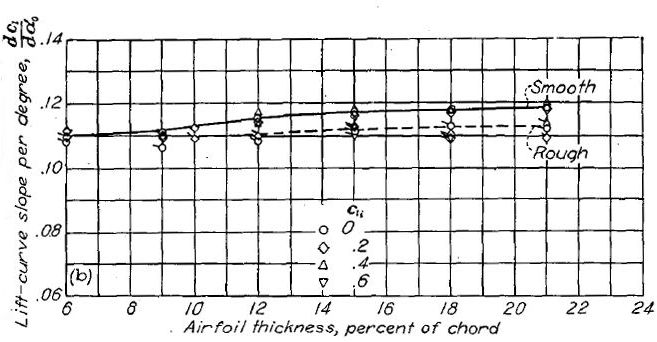
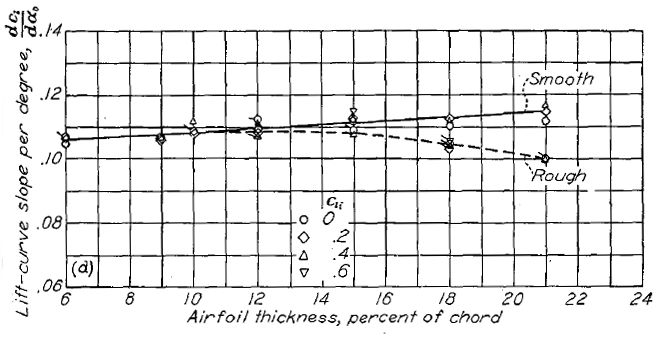
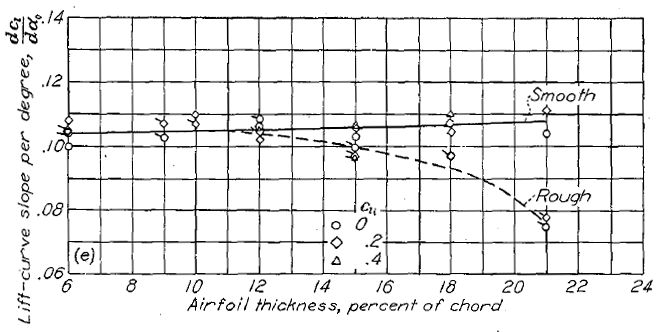
ラングレイの二次元低乱流圧力風洞でテストされた翼型の揚力曲線傾斜(lift-curve slope, Figure.38)は、これまでに知られていた数値(資料 8)よりも高い値を示している。資料 8 のアスペクト比は 6 とされており、この差異が乱流の存在によるものか試験手法の違いによるものかは判然としない。Figure.38 に示されたデータはレイノルズ数 6x10
6、揚力係数は翼型の設計揚力係数にほぼ一致する値として計測されている。NACA 6- シリーズの場合、これは低抵抗域のほぼ中心である。翼厚比 6〜10% の場合、NACA 4 桁、5 桁および 64- シリーズの揚力曲線傾斜は薄翼に非常に近い値を取る(2π/rad あるいは 0.0110/deg)。3x10
6〜9x10
6 のレイノルズ数域において、翼弦 4% までのキャンバー変化は揚力曲線傾斜に系統的な影響を与えていない。翼厚比および厚み分布が支配的な影響をもたらす。NACA 4 桁および 5 桁翼型については、翼厚比の増加にともなって揚力曲線傾斜が低下する。NACA 6- シリーズ翼型についてはしかし、翼厚比の増加およびゼロ揚力における基準翼型の最小圧力位置の前進に応じて揚力曲線傾斜が増大する。
 (a) NACA 4 および 5 桁 (a) NACA 4 および 5 桁 |
 (b) NACA 63- シリーズ (b) NACA 63- シリーズ |
 (c) NACA 64- シリーズ (c) NACA 64- シリーズ |
 (c) NACA 65- シリーズ (c) NACA 65- シリーズ |
 (e) NACA 66- シリーズ (e) NACA 66- シリーズ |
|
Figure.38 平滑状態と荒面状態における各種 NACA 翼型の翼厚・キャンバーと揚力曲線傾斜の相関。R=6x106.
いくつかの NACA 6- シリーズの揚力曲線は低抵抗域の終端付近において、特に小レイノルズ数域において揺らぎ(jog)を見せる。揺らぎはキャンバーが大きいほど、また基準翼型の最小圧力位置が後方に寄るほどに大きくなる。揺らぎはレイノルズ数の増大と共に急速に減少して揚力曲線傾斜の変化となり、9x106 付近ではほぼ消失する。この揺らぎは低速の小型機における翼型選定において考慮されるべきであろう。この揺らぎの発生源となる流れの解析について資料 28 に示す。
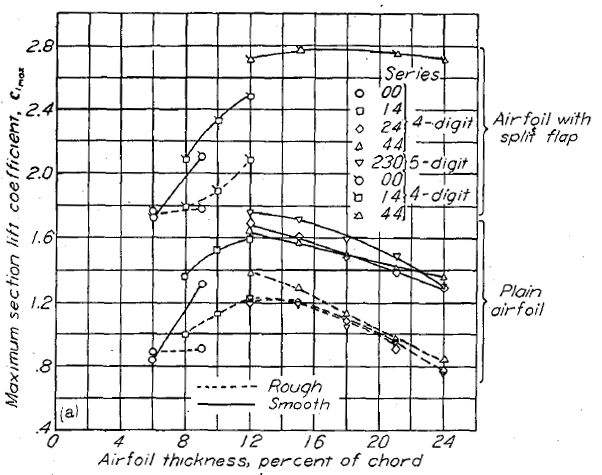
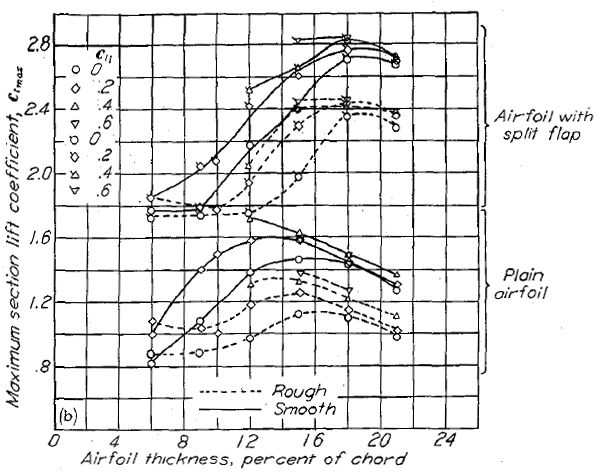
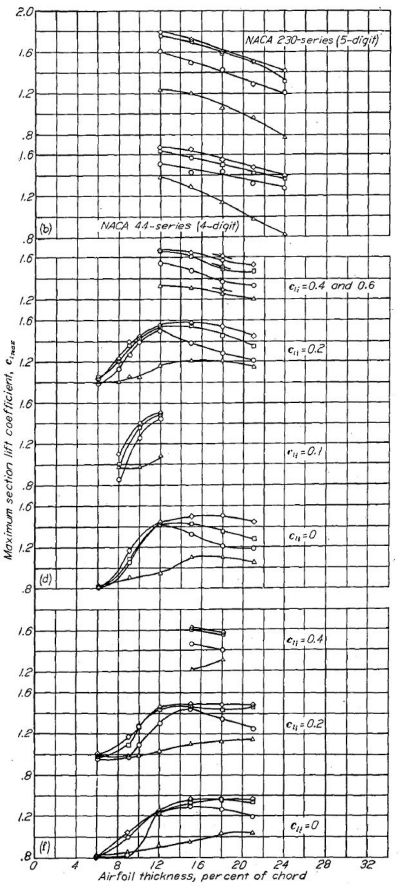
レイノルズ数 6x106 における、各種 NACA 翼型および翼厚比における最大揚力係数を Figure.39 に示す。ここに示した翼型は翼厚比 6〜24%、キャンバーは翼弦 4% までのものである。NACA 4 桁および 5 桁の翼型(Figure.39(a))については、通常の(フラップを伴わない)最大揚力係数は翼厚比 12% において得られる。総じて、翼厚比と最大揚力係数の相関は翼厚比 12% 未満において最大となる。NACA 6- シリーズ翼型(Figure.39(b)〜(e))についても、翼厚比増大に伴う最大揚力係数の増加は 12% 未満において急激である。設計揚力係数 0.2 未満の NACA 6- シリーズ翼型について、揚力係数が最適となる翼厚比は、最小圧力位置が翼弦 60% の場合を除き 12〜15% である。設計揚力係数 0.2 未満の NACA 66- シリーズの場合、揚力係数が最適となる翼厚比は 15% 以上である。得られたデータは揚力係数 0.4 の場合翼厚比 12% 未満が最適であることを示している。
翼厚比 6, 8, 21% の基本翼型データは、最大揚力係数が最小圧力位置の変化に対して鈍感であることを示している。翼厚比が中程度の場合、特に設計揚力係数 0.2 の場合、最大揚力係数は最小圧力位置の前進に応じて増大する。
中程度のキャンバーを持つ NACA 6- シリーズ翼型では、最大揚力係数はキャンバーの増加に応じて増大する(Figure.39(b)〜(e))。翼厚比 6〜12% の範囲で、対称翼に対するキャンバーの付与は最大の最大揚力係数増大を示す。キャンバーによる最大揚力係数増大は翼厚比 12〜15% を過ぎると効果が減少する。得られたデータによれば、翼厚比 12%、設計揚力係数 0.4 の基準線キャンバー(mean line camber)を持つ翼型が最も高い最大揚力係数を持つことを示している。
 (a) NACA 4 および 5 桁 (a) NACA 4 および 5 桁 |
 (b) NACA 63- シリーズ (b) NACA 63- シリーズ |
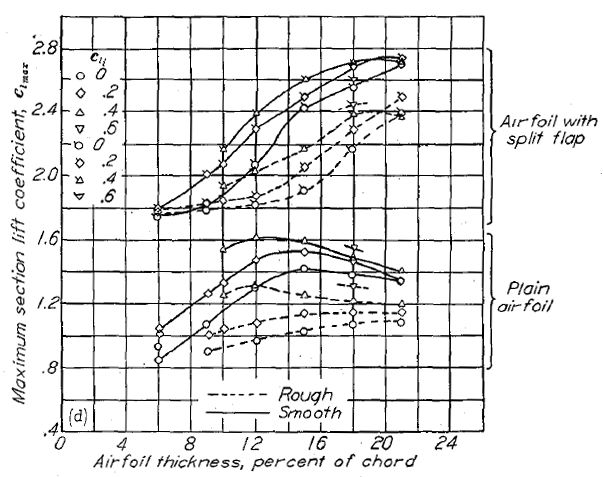 (c) NACA 64- シリーズ (c) NACA 64- シリーズ |
 (c) NACA 65- シリーズ (c) NACA 65- シリーズ |
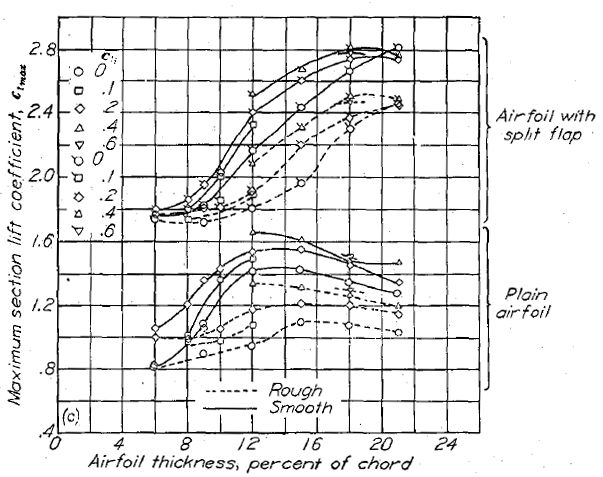 (e) NACA 66- シリーズ (e) NACA 66- シリーズ |
|
Figure.39 平滑状態と荒面状態における、フラップ未使用・使用時の各種 NACA 翼型の翼厚・キャンバーと最大揚力係数の相関。R=6x106.
6- シリーズの翼厚分布を持つ翼型について、基準線(mean line)と最大揚力係数の相関を Figure.40 に示す。αが 0.5 未満の基準線については系統的なデータがない。しかしながら、NACA 230- シリーズのように最大キャンバーが前寄りの翼型は高い最大揚力係数を示していることを注記しておく。最大キャンバーが前寄りで翼厚比 6〜12% の翼型はふつう前縁から失速し、急激で大きな揚力損失をもたらす。より望ましい緩やかな失速は最大キャンバーを後ろにずらした通常キャンバー(Normal type of camber)の NACA 24-, 44- および 6- シリーズのような翼型によって得られる。
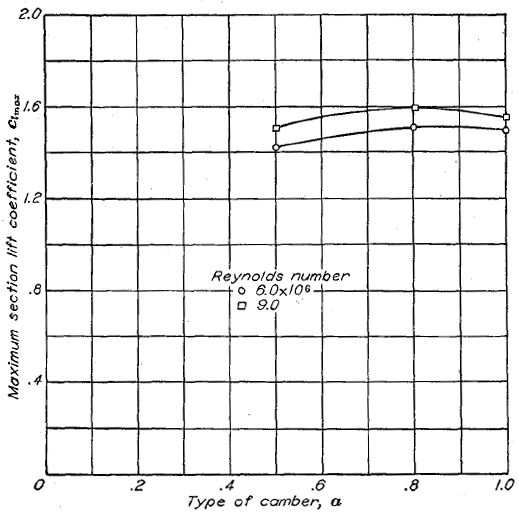 Figure.40 ラングレイ二次元低乱流圧力風洞で得られた NACA 653-418 翼型のキャンバーと最大揚力係数の相関。
Figure.40 ラングレイ二次元低乱流圧力風洞で得られた NACA 653-418 翼型のキャンバーと最大揚力係数の相関。
設計揚力係数 0.4 のキャンバーを持つ NACA 64- シリーズ翼型と NACA 44- および 230- 翼型の最大揚力係数の比較(Figure.39)を見ると、ほぼ全ての状況において 64- シリーズの最大揚力係数は 44- シリーズを上回る。NACA 230- シリーズの最大揚力係数は 64- シリーズよりやや高い。
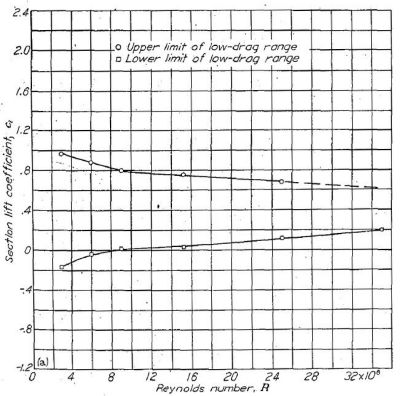
レイノルズ数 3x106〜9x106 における、各種 NACA 翼型のスケール効果を Figure.41 に示す。NACA 24-, 44-, 230- シリーズのスケール効果(Fiure.41(a)(b))は翼厚比 12〜24% において好ましく、翼厚比とはほぼ無関係である。レイノルズ数を 3x106 から 9x106 に増大させた場合、最大揚力係数は約 0.15 から 0.20 まで増大する。NACA 00- および 14- シリーズ翼型のスケール効果は、翼厚比 0.12c 以下において非常に小さい。
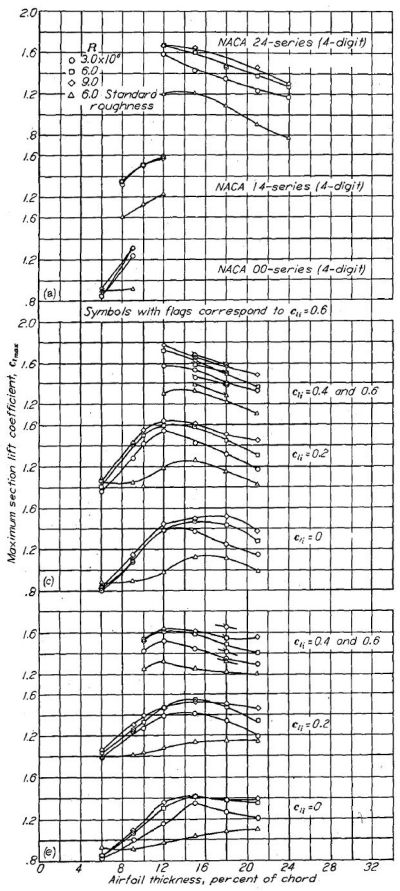 |
 |
(a) NACA 4 桁
(c) NACA 63- シリーズ
(d) NACA 65- シリーズ
|
(a) NACA 4 および 5 桁
(c) NACA 64- シリーズ
(d) NACA 66- シリーズ
|
Figure.41 異なるキャンバーを持つ NACA 各種翼型によるレイノルズ数と最大揚力係数と翼厚比の相関。
図をクリックすると別ウィンドウに拡大表示
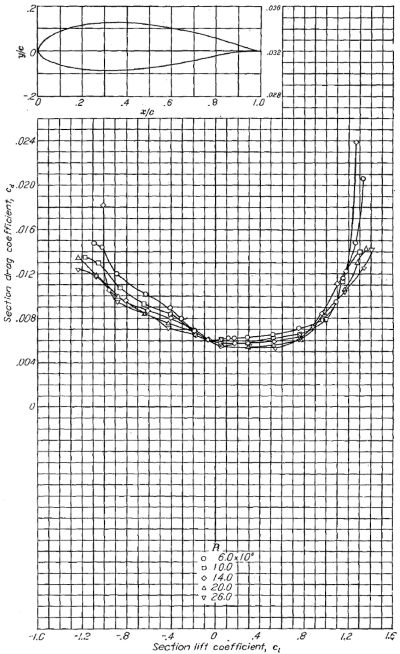
NACA 6- シリーズのスケール効果(Figure.41(c)〜(f))は必ずしも一定の傾向を示していない。総じて、スケール効果は好ましい方向に出ている。NACA 63- および 64- シリーズのキャンバーの小さな翼型では、翼厚比 12% 未満においてレイノルズ数増大に伴う最大揚力係数の増加は全体的に小さいが、翼厚比が大きくなると影響も大きくなる。NACA 65- および 66- シリーズもおおむね 63- および 64- シリーズと同等の傾向を示すが、傾向はそれほど顕著ではない。ほとんどの場合において、設計揚力係数 0.4〜0.6 の NACA 6- シリーズ翼型のスケール効果は翼厚比の影響を受けない。Figure.42 は NACA 63(420)-422 翼型の最大揚力係数をレイノルズ数 26x106 まで示したものである。
Figure.42 大レイノルズ数域における NACA 63(42)-422 翼型の揚力および抗力特性。TDT tests 228 and 225。
図をクリックすると別ウィンドウに拡大表示
ここで示された最大揚力係数の数値は安定した状態(steady conditions)で計測されている。最大揚力係数は迎角の増大によってより増加するであろう。このような状態は突風や着陸時の機動に伴って発生すると考えられる(資料 41 を参照のこと)。
NACA 6- シリーズの翼型研究は下げ角 60 度までの模擬スプリット・フラップを含んでいる。これらの研究はより効果的な高揚力装置の必要性を示唆するであろうと考えられていたが、この仮説を裏付けるに足るデータは得られていない。模擬フラップを含む各種翼型の最大揚力係数データを Figure.39 に示す。
NACA 00- および 14- 翼型においてスプリット・フラップは著しい最大揚力係数の増加を見せ、この傾向は翼厚比の増大に伴って大きくなる。これに相応する NACA 44- シリーズのデータは、翼厚比 12〜24% の範囲において翼厚比と最大揚力係数の相関はほとんど見られない。NACA 6- シリーズにおいては、ある翼厚比を超えた段階から急激な揚力係数の増大が見られ、この翼厚比はキャンバーによって 6〜9% となる。この上限は NACA 64- および 65- の対称翼において 21% 以上、NACA 63- および 66- 翼型において約 18% である。翼厚比 6〜9% の範囲において、NACA 6- シリーズの対称翼型の最大揚力係数は翼厚比および最小圧力位置位置に関わらずほぼ同じである。翼厚比 9〜18% において、最大揚力係数は最小圧力位置位置の後退に伴って減少する。
中程度(翼弦 10〜15%)の翼厚比を持つ NACA 6- シリーズ翼型において、フラップ使用時の最大揚力係数はキャンバー増大に伴って著しく増大する。翼厚比 6% あるいは 18〜21% の場合、最大揚力係数はほとんどキャンバーの影響を受けない。翼厚比 15%、設計揚力係数 0.4 のキャンバーを持つ NACA 63- および 64- シリーズ翼型において、フラップ使用時の最大揚力係数はこれに相当する 44- シリーズ翼型よりも大きくなる。
三次元データ(Three-dimentional data)
大レイノルズ数域での三次元翼については最新の系統的なデータがなく、翼型実験との比較は困難である。三次元翼における最大揚力を翼型データと比較する場合、翼幅方向の荷重分布が考慮される必要がある。翼幅方向の荷重分布は一様ではないため、三次元翼における最大揚力係数は翼型データよりも低くなるであろう。その差はアスペクト比 6 の矩形翼で 4〜7% となる。
ライングレイの 19 フィート圧力風洞で計測された各種翼型の最大揚力データを表 II に示す。同レイノルズ数域における翼型データとの厳密な比較ができるほど充実はしていないが、通常の(フラップを出していない)翼型について表 II のデータは概ね翼型データから期待される値を示している。飛行機模型のデータは各種の翼型と装着状態における最大揚力係数を示している。
不平滑翼型の揚力特性(LIFT CHARACTERISTICS OF ROUGH AIRFOILS)
二次元データ(Two-dimentional data)
近年に行われた翼型のテスト、特に翼厚比の大きな翼型については、前縁を荒らした状態でのデータが付録図に含まれている(資料 37)。
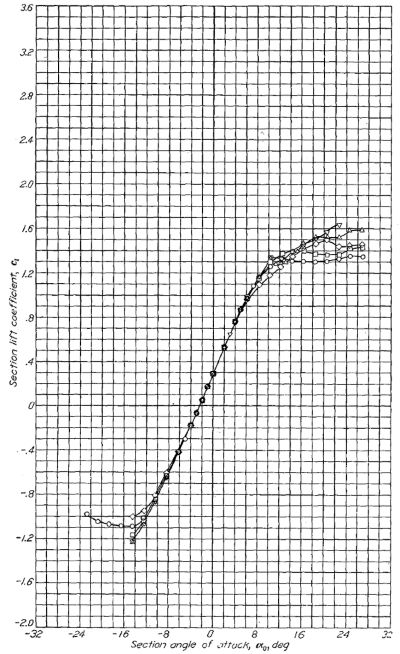
Figure.43 に、NACA 63(420)-422 翼型における、前縁の荒度を変化させた場合の最大揚力係数への影響を示す。どの前縁状態においても、最大揚力係数はレイノルズ数の増大に伴って漸増する(Figure.43)。Figure.24 は前縁 20% に置いた荒面帯が最大揚力係数や揚力曲線傾斜にはほとんど影響を与えていないことを示している。Figure.38 に示された実験結果は、前縁に置いた標準荒面帯が揚力曲線傾斜を減少させ、これは特に最小圧力位置を後退させた翼厚比の厚い翼型において顕著なことを示している。これらのデータはレイノルズ数 6x106 で計測された。
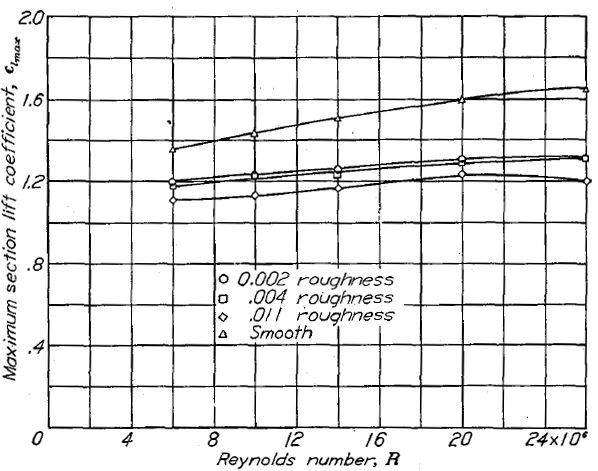 Figure.43 平滑前縁と荒れ前縁を持つ NACA 63(420)-422 翼型におけるレイノルズ数と最大揚力係数 Clmaxの相関。
Figure.43 平滑前縁と荒れ前縁を持つ NACA 63(420)-422 翼型におけるレイノルズ数と最大揚力係数 Clmaxの相関。
標準荒面帯を前縁に置いた状態で、レイノルズ数 6x106 における各種翼型の最大揚力係数を Figure.39 および Figure.41 に示す。NACA 4 桁および 5 桁翼型については、翼厚比と最大揚力係数の相関は平滑翼型とほぼ同じ傾向を示しているが、翼厚比 6% の場合は NACA 00- 翼型を除いて著しく低い値となっている。15% 以上の翼厚比については、4 桁と 5 桁翼型の最大揚力係数は概ね同じである。
NACA 6- シリーズにおいては、翼厚比と最大揚力係数の相関に前縁荒面帯の有無がもたらす影響はより小さい。翼厚比 6% の場合、最大揚力係数は前縁荒面帯の有無に関わらずほぼ同じである。キャンバーと最大揚力係数の相関はしかし、前縁荒面帯のある場合と平滑な場合でおおむね同じである。前縁荒面帯を付けた翼型では、最大揚力係数は最小圧力位置の後退に伴って減少するが、翼厚比 18% 以上の場合は最小圧力位置の後退に伴って最大揚力係数はやや増大する。
前縁荒面帯を付けた場合、設計揚力係数 0.4 のキャンバーを持つ NACA 64- シリーズ翼型は、翼厚比 12〜15% の NACA 44- シリーズ翼型を除けば、同程度の翼厚比を持つ NACA 24-, 44-, 230- シリーズ翼型よりも高い最大揚力係数を示している。スプリット・フラップ使用時の標準前縁荒面帯による最大揚力係数の減少は、フラップ未使用時の場合と概ね同じ傾向を示す。
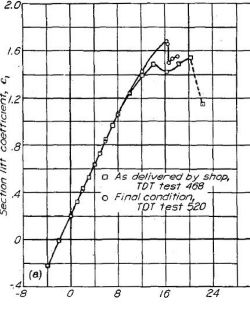
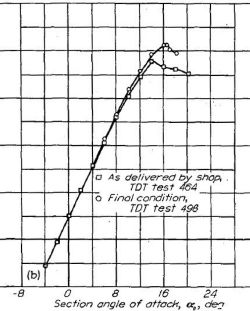
主翼前縁の曲面形成の歪みは最大揚力係数の減少を引き起こすと考えられるが、系統的なデータは得られていない。偶然得られたケースを Figure.44 に示す。これは正確な翼型モデルと不正確なモデルの揚力特性を示したものであるが、歪みは非常に小さなものであったため、以前のテストでは検出できていなかった。
 (a) NACA 2412 (a) NACA 2412 |
 (b) NACA 2415 (b) NACA 2415 |
 (c) NACA 23012 (c) NACA 23012 |
Figure.44 模型の不正確さによる NACA 23012, 2412, 2415 翼型への揚力特性。R=約9x106.
図をクリックすると別ウィンドウに拡大表示
三次元データ(Three-dimentional data)
ラングレイの実機大風洞における何機種かの実験結果(資料 42)は、実機における最大揚力係数は翼型以外の要因が多く相関することを示している。それらの要因とは表面平滑度、気流漏れ、前縁吸気口、兵装、ナセル、胴体などであり、たとえフラップを引きこんだ場合であっても、翼型と全機揚力係数の相関算出を困難にしている。各種フラップ実装方式の相違は、フラップ使用時の相関を更に困難なものにする。フラップを引きこんだ場合については、NACA 6- シリーズ翼型を使用した機体について実機での最大および最小揚力係数と、飛行状態における木型模型のラングレイ実機大風洞におけるデータが得られている。
ラングレイの 19 フィート圧力風洞における木型模型と、実機大風洞における実機測定の結果を Figure.45 に示す。両者のテストにおいてレイノルズ数は概ね同じである。テスト結果は前線状態にある実機の揚力係数は木型模型より約 0.2 低く、揚力曲線傾斜も低いことを示している。実機の特性は気流漏れの封止によって多少の改善が見られた。これらの結果は、実機の揚力特性は平滑な大型模型では再現されない細部の仕上げによって大きな影響を受けることを示している。
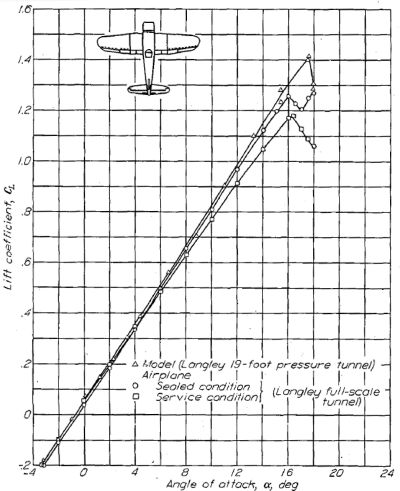 Figure.45 戦闘機タイプの航空機に表面状態が与える揚力の影響。R=2.8x106.
Figure.45 戦闘機タイプの航空機に表面状態が与える揚力の影響。R=2.8x106.
図をクリックすると別ウィンドウに拡大表示
Figure.46 と Figure.47 は、ラングレイの 19 フィート圧力風洞において、主翼前桁位置に遷移源を置いた場合とそうでない場合の木型模型の特性比較を示している。どちらの場合も遷移源によって揚力曲線傾斜は下がっているが、最大揚力係数は1例では減少し、1例では増大している。
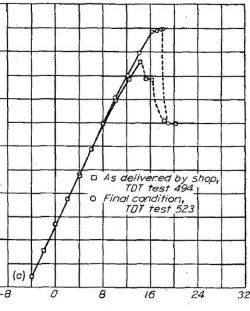
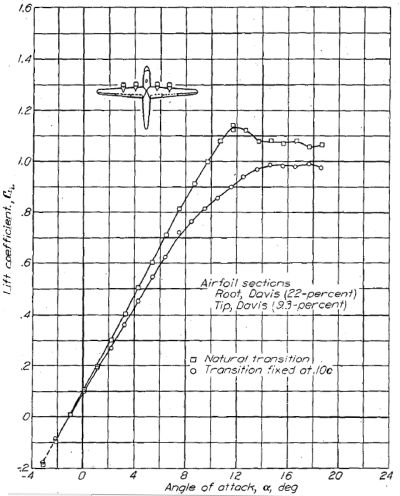 Figure.46 ラングレイ 19 フィート圧力風洞にける Figure.46 ラングレイ 19 フィート圧力風洞にける
模型に対する固定遷移の影響。R=2.7x106. (デイビス翼型)
図をクリックすると別ウィンドウに拡大表示
|
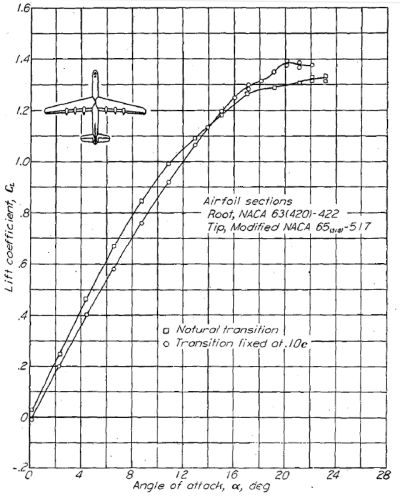 Figure.47 ラングレイ 19 フィート圧力風洞にける Figure.47 ラングレイ 19 フィート圧力風洞にける
模型に対する固定遷移の影響。R=2.7x106. (NACA 翼型)
図をクリックすると別ウィンドウに拡大表示
|
保守的でない翼型(UNCONSERVATIVE AIRFOILS)
特に長距離飛行を目的とする抵抗減少のため、高翼面荷重と低翼幅荷重を組み合わせることが行われている。その結果はアスペクト比が高く、合理的な強度構造のため主翼桁の深い主翼となり、深い主翼桁によって主翼基部の翼厚が厚くなる。
主翼基部を厚くする流行は平滑翼面での低抵抗係数(Figure.12)によって推進されたものだが、実機の主翼は翼型模型のように平滑ではなく、また前線使用状態では平滑さを保つことも期待しがたい。前縁荒れは翼厚比の厚い翼型では特に、高揚力係数時に大きな抗力係数の増加をもたらす。この抗力係数の増大は、高翼面荷重の高々度巡航にも大きな影響を与えるであろう。平滑時には理想的な特性を示すが、表面荒れによって巡航あるいは上昇時に大きな抵抗をもたらす翼型を「保守的でない(Unconservative)」と分類される。
ある翼型が保守的でないか否かの判定は、それが用いられる飛行機の出力と翼面荷重に依存する。また、運用と保守の状況も考慮されるべきであろう。例えば翼面に氷が付着するような状況で多発機に片発停止飛行するとか、戦闘損傷を受けた場合などである。
翼型の保守性に関する判断材料として、多数の NACA 翼型に前縁荒面帯を付けた場合の付録図から、抗力係数 0.02 に相当する揚力係数を使用することとした。この臨界揚力係数(Critical lift coefficient)と翼厚比・キャンバーの相関を Figure.48 に示す。このデータは全体的に、抗力係数 0.02 に相当する揚力係数が最小圧力位置の後退に伴って低下することを示している。揚力係数が最大となる翼厚比は概ね 12〜15% の間であり、これを超えると急激な臨界揚力係数の低下をもたらす。キャンバーの付加は一般に臨界揚力係数の増大をもたらすが、非常に厚い主翼の場合は効果は少なく、むしろ弊害になる可能性もある。Figure.48 のデータはレイノルズ数 6x106 で計測された。Figure.49 に示すように、表面荒れが前縁にとどまる場合、飛行レイノルズ数域における抗力係数は 6x106 の場合よりずっと低いことも考えられる。
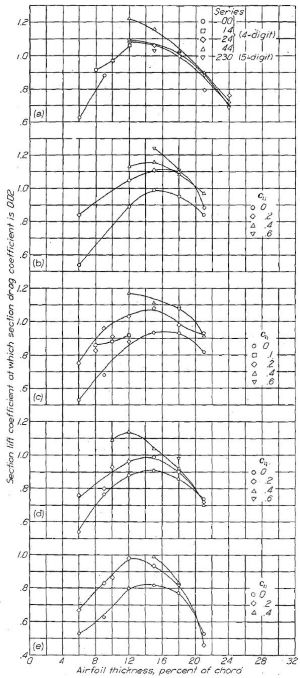 (a) NACA 4 および 5 桁
(a) NACA 4 および 5 桁
(b) NACA 63- シリーズ
(c) NACA 64- シリーズ
(d) NACA 65- シリーズ
(e) NACA 66- シリーズ
Figure.48 平滑と荒らした前縁を持つ各種翼厚比・キャンバーの NACA 翼型における、抗力係数 0.02 に相当する揚力係数の特性。R=6x106.
図をクリックすると別ウィンドウに拡大表示
Figure.49 前縁荒面帯を付けた NACA 65(223)-422(改) 翼型の揚力と抵抗の特性。
図をクリックすると別ウィンドウに拡大表示
ピッチング・モーメント(PITCHING MOMENT)
(省略)
空力中心位置(POSITION OF AERODYNAMIC CENTER)
(省略)
高揚力装置(HIGH-LIFT DEVICES)
(省略)
横方向の操縦機構(LATERAL-CONTROL DEVICES)
(省略)
前縁吸気口(LEADING-EDGE INTAKES)
(省略)
干渉(INTERFERENCE)
(省略)
主翼設計への適用(APPLICATION TO WING DESIGN)
主翼設計に関わる様々な要因については本報告書の範疇を超える。下記の議論はあくまで、本報告書において示された主翼設計上重要な空力的特性についてのみ言及している。
翼型の適用(APPLICATION OF SECTION DATA)
主翼の特性は通常、翼型の線揚力理論(simple lifting-line theory, 資料 73〜76)によって推測される。翼幅方向の不連続性を考慮に入れなくとも、この方法によってある程度は正確な予測が可能であり(資料 77)、これは特にゼロ揚力、揚力曲線傾斜、ピッチングモーメント、抵抗などの重要な特性について当てはまる。線形翼型揚力特性(linear section lift characteristics, 資料 78〜79)を考慮した場合は、特に高揚力係数域においてより精度を高めることができる。翼幅方向の揚力分布(資料 80)を考慮することによって更に改善できる。大きな後退角を持つ翼については特別な配慮が必要である(資料 81)。
通常の翼理論では、翼型の発生する空力とモーメントは翼型形状と揚力係数(あるいは迎角)のみによって決定される。この前提に従うならば、空力やモーメントは隣接する翼型や翼の付加機能(それが翼型や迎角を変えるようなものでない限り)の影響を受けないことになる。この前提は明らかに、翼端近傍やフラップ・エルロンなどの不連続部、胴体との干渉乱流部、平面形の屈曲部、継ぎ目や捩じりのある翼については適用できない。このような部位では交叉流(cross flows)が発生し二次元翼型の前提は成立しなくなり、また交差流に加えてキャンバーの変化と同等の効果が誘因される。このような効果は通常の平面形翼では翼端部、アスペクト比の小さな翼、あるいは異例な平面形において顕著となる。面揚力理論(lifting-surface theory, 資料 81)は、単純な線揚力理論よりも高精度な翼特性の算出式を与える。
部分翼幅のフラップのような不連続性を含む翼幅方向の荷重分布の計算(資料 82, 83)は構造強度設計には充分な精度を持つが、このような計算は最大揚力や失速特性を試算するには不十分である。不連続性を持つ翼の最大揚力や失速特性について充分な知見が蓄積されるまでは、このような特性は類似の前例から予測するか、異例な形状の場合は実験によって確認すべきであろう。
主翼中央部の翼型についても翼型理論が適用されるべきであるが、不十分なデータしか揃っていない。幾つかの製造元による直線フェアリングを持つ翼の実験結果は、中央部のデータは翼根部と翼端部の翼型と翼厚分布からの補間によってある程度の精度で予測可能なことを示している。
翼根部翼型の選択(SELECTION OF ROOT SECTION)
主翼の特性は翼根部に大きな影響を受ける。直線テーパー翼の場合は翼端に向かって翼型が変化してゆくが、主翼の大部分は翼根部の翼型に支配される。燃料や機材の格納、あるいは翼幅を確保するため、翼根部は可能な限り厚くすることが望まれることが多い。翼厚に対して抵抗係数は大きく変化しないこと、フラップによる大揚力が求められることから、翼根部の選択は最大揚抗比以外の特性で決定される。
高速機においては臨界マッハ数が最も深刻な制限になる。翼根部には胴体との干渉による流速増大が発生するため、想定される運用速度よりも大幅に臨界マッハ数の高い翼型の選択が望まれる。現在得られるデータは、臨界マッハ数と抵抗が急増するマッハ数の間にはわずかなマージンがあることを示す。航空機の速度がより高くなれば、薄翼化による抵抗急増を避けることは次第に困難になり、遂には不可能になる。
圧縮性の影響を考えない速度域の航空機においては、翼厚の限界は中〜高揚力時における、とりわけ表面が不平滑である場合の抵抗の増大によって制限される。翼型の選択は実機での表面状態が考慮されなければならない。軍用機においては特に泥や氷の付着や戦闘破損、多発機における片発飛行が考慮されなければならない。アスペクト比の増加を目的として翼根部を厚くする場合も、中〜高揚力時における現実的な表面処理状態における抵抗係数によって最適アスペクト比が定まり、それを超えて厚翼化しても性能はかえって低下する。
通常の航空機において翼根部はプロペラ後流の中にあって胴体とも干渉し、脚や兵装や整備パネルなども設けられる。そのため翼根部では層流効果を期待しがたい。このような条件が緩和されないかぎり、層流翼による抵抗削減は望めない。もし翼根部の厚みが大きい場合、大きな層流効果に期待しない 63- シリーズが優位を提供するであろう。
翼端部翼型の選択(SELECTION OF TIP SECTION)
良好な失速特性を実現するため、翼端部には大揚力係数と大きな迎角幅を持つ翼型が望まれる。失速特性も急峻でないことが望ましい。テーパー翼では翼端部のレイノルズ数が減少するため、大揚力係数の実現は翼根部よりも困難な場合が多い。このような場合、翼端部のキャンバー(曲率)を増加することが揚力係数増加に効果的である。多くの場合、キャンバーは高速時の抵抗特性や臨界速度の要求によって制限される。
翼端部のキャンバー選択は既存データから回答を得がたい困難を伴う。キャンバーによっては補助翼に大きな負荷が生じて横操縦性の困難と重量増大を招く。揚力中心を前進して補助翼の負担を減らすタイプのキャンバーは往々にして揚力係数を大して増大しない。NACA 230- シリーズのように最大キャンバーが前寄りの翼型では揚力係数も期待できるが、この場合は失速時に急激な揚力の減少が起き得る。エルロンによる主翼後縁キャンバーの変化に伴う主翼特性の影響は決して軽視してはならない。
翼根部がじゅうぶん厚い場合、翼端部では翼厚比をある程度減らすことが望まれる。翼端部では胴体の干渉を受けないため、薄翼化することによって同じ臨界速度においてもより大きなキャンバーを与えることができる。薄翼化の限界は揚力係数によって制限されるであろう。
失速の抑制にはねじり下げ(Washout)も有効である。ねじり下げの限界は誘導抵抗によって制限されるが、1〜2 度の範囲ではその影響は小さい(資料 73)。ねじり下げはまた、高速飛行時に翼端部が低抵抗領域を逸脱してしまうことによっても制限される。翼型によっては、キャンバーを調整しなければねじり下げを与えることができない場合もある。
翼根部と翼端部で翼型を変えることは失速特性の改善と、翼端部で期待できる層流効果の活用に望ましい。例えば翼根部 NACA 230- +翼端部 NACA 44-、あるいは翼根部 NACA 63- + 翼端部 NACA 65- などが望ましいであろう。
翼型の選択やねじり下げの処理が適切でない限り、翼端部はいとも簡単に過大な負荷がかかって翼端失速を招く。この点において、過大なテーパー比や大きな後退角は望ましくない。この両者を組み合わせることは最悪であり、これによって引き起こされる翼端失速は横方向だけでなく縦方向の不安定性も招く。
結論(CONCLUSIONS)
これまでのデータから、以下の結論が導き出せる。なお揚力、抗力、ピッチングモーメントなどの特性は 3〜9x106 のレイノルズ数域によって測定されている。
1. 翼面が平滑である限り、NACA 6- および 7- シリーズのような層流翼型は、高速飛行および巡航飛行での揚力係数域において、他の翼型より大幅な抗力の減少が実現できる。
2. 実機サイズの翼型模型を用いた場合、320 番のサンドペーパーで翼弦方向に研磨した程度の平滑度でも広範囲の層流を実現できる。また翼型の波打ちについては、前縁に直線定規を当てて滑らかに動く程度の仕上げ精度でも満足すべき結果が得られる。
3. 現在の航空機製造法に基づく中程度の翼厚比では、最小抵抗係数は 0.0080 程度が期待される。このような翼において、最小抵抗係数は翼型よりも表面仕上げ精度によって影響される。
4. 翼面の平滑化はたとえ広範囲の層流が実現できなくとも、大レイノルズ数域における抵抗削減に大きな効果がある。
5. 中程度のキャンバーを持つ NACA 6- シリーズの層流翼型の最大揚力係数は、NACA 24- および NACA 44- シリーズと大差ない。NACA 230- シリーズの揚力係数は 0.2 未満の翼厚比においてやや高い。
6. 中程度に厚い NACA 6- シリーズ層流翼のフラップによる最大揚力係数は NACA23012 と大差ないが、翼厚比が薄くなると大幅に低くなる。
7. NACA 6- シリーズの揚力曲線傾斜は NACA 24-, 44-, 230- シリーズよりやや高く、薄翼については理論値を上回る場合が多い。
8. 前縁部の表面乱れはフラップなし・60度下げいずれの場合も最大揚力係数の大幅な減少をもたらす。標準荒面帯による揚力係数の減少はフラップなし・60度下げの場合でほぼ同じである。
9. 前縁部の表面乱れは揚力傾斜の減少をもたらし、これは最小圧力位置を後ろに置いた翼型においてより顕著である。
10. 翼型特性を実機製法において期待される仕上げ条件で計測することは、実機の性能を予測する上で重要である。
11. 高速飛行および巡航飛行時の揚力係数域において、NACA 6- シリーズは従来翼型よりも臨界マッハ数が高く、臨界マッハ数域において充分な揚力係数を実現できる。
12. 中程度以上の揚力係数域においては、NACA 6- シリーズの臨界マッハ数は従来翼型に比べてそれほど高くない。しかし不十分なデータではあるが、臨界マッハ数域における NACA 6- シリーズの揚力係数は従来翼型に比べて満足できるものである。
13. NACA 6- シリーズ翼型は補助翼の装備について困難は認められない。
14. NACA 6- シリーズの干渉による境界層の剥離特性は、他の良好な翼型と同様である。剥離拡大を防ぐ最適なフィレット形状は場合によって異なるであろう。
15. NACA 6- シリーズには満足すべき前縁インテイクを設けることができるが、定番というべき手法は確立されておらず、実験に頼る必要がある。
LANGLEY MEMORIAL AERONAUTICAL LABORATORY
NATIONAL ADVISORY COMMITEE FOR AERONAUTICS
LANGLEY FIELD, VA. March 5, 1945.